| –†–Α―¹–Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ–Β–Ϋ–Η–Β ―Ä–Α–¥–Η–Ψ–≤–Ψ–Μ–Ϋ –≤ –Ω–Μ–Α–Ζ–Φ–Β. –™–Β–Ϋ–Β―Ä–Α―Ü–Η―è ―Ä–Α–¥–Η–Ψ–Η–Ζ–Μ―É―΅–Β–Ϋ–Η―è –Ω–Μ–Α–Ζ–Φ–Β–Ϋ–Ϋ―΄–Φ–Η –Κ–Ψ–Μ–Β–±–Α–Ϋ–Η―è–Φ–Η |
| –ù–Α―É–Κ–Α - –†–Α–¥–Η–Ψ–Α―¹―²―Ä–Ψ–Ϋ–Ψ–Φ–Η―è |
|
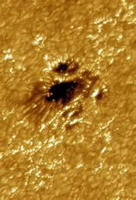
–ü―É―¹―²―¨ –Ϋ–Α –Ψ–±–Μ–Α–Κ–Ψ –Ω–Ψ–Μ–Ϋ–Ψ―¹―²―¨―é –Η–Ψ–Ϋ–Η–Ζ–Ψ–≤–Α–Ϋ–Ϋ–Ψ–≥–Ψ –≥–Α–Ζ–Α (–Ω–Μ–Α–Ζ–Φ―΄) –Ω–Α–¥–Α–Β―² –Ω–Μ–Ψ―¹–Κ–Α―è –Φ–Ψ–Ϋ–Ψ―Ö―Ä–Ψ–Φ–Α―²–Η―΅–Β―¹–Κ–Α―è –≤–Ψ–Μ–Ϋ–Α, ―Ä–Α―¹–Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―è―é―â–Α―è―¹―è –≤–¥–Ψ–Μ―¨ –Ψ―¹–Η z. –≠–Μ–Β–Κ―²―Ä–Η―΅–Β―¹–Κ–Ψ–Β –Ω–Ψ–Μ–Β –≤–Ψ–Μ–Ϋ―΄ ¬†–ü–Ψ–¥ –¥–Β–Ι―¹―²–≤–Η–Β–Φ ―ç―²–Ψ–≥–Ψ –Ω–Ψ–Μ―è ―ç–Μ–Β–Κ―²―Ä–Ψ–Ϋ―΄ –Ω―Ä–Η―Ö–Ψ–¥―è―² –≤ –¥–≤–Η–Ε–Β–Ϋ–Η–Β. –ö–Μ–Α―¹―¹–Η―΅–Β―¹–Κ–Ψ–Β ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β –¥–≤–Η–Ε–Β–Ϋ–Η―è ―ç–Μ–Β–Κ―²―Ä–Ψ–Ϋ–Α: m βÄ™ –Φ–Α―¹―¹–Α ―ç–Μ–Β–Κ―²―Ä–Ψ–Ϋ–Α, n―¹―² βÄ™ ―΅–Α―¹―²–Ψ―²–Α ―¹―²–Ψ–Μ–Κ–Ϋ–Ψ–≤–Β–Ϋ–Η–Ι –≤ –Ω–Μ–Α–Ζ–Φ–Β (–≤―²–Ψ―Ä–Ψ–Β ―¹–Μ–Α–≥–Α–Β–Φ–Ψ–Β –≤ –Μ–Β–≤–Ψ–Ι ―΅–Α―¹―²–Η ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η―è –Ψ–Ω–Η―¹―΄–≤–Α–Β―² ―²―Ä–Β–Ϋ–Η–Β ―ç–Μ–Β–Κ―²―Ä–Ψ–Ϋ–Α –Ψ–± –Ψ–Κ―Ä―É–Ε–Α―é―â―É―é –Ω–Μ–Α–Ζ–Φ―É, –Ω―Ä–Η–≤–Ψ–¥―è―â–Β–Β –Κ –Ζ–Α―²―É―Ö–Α–Ϋ–Η―é –Κ–Ψ–Μ–Β–±–Α–Ϋ–Η–Ι). –ù–Α–Ω–Ψ–Φ–Ϋ–Η–Φ ―²–Α–Κ–Ε–Β ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η―è –€–Α–Κ―¹–≤–Β–Μ–Μ–Α: –£ –¥–Α–Μ―¨–Ϋ–Β–Ι―à–Β–Φ –¥–Μ―è –Ω―Ä–Ψ―¹―²–Ψ―²―΄ ―¹―²―Ä–Β–Μ–Κ–Η –Ϋ–Α–¥ –≤–Β–Κ―²–Ψ―Ä–Α–Φ–Η –Ψ–Ω―É―¹–Κ–Α–Β–Φ. –ü―Ä–Η ―Ä–Β―à–Β–Ϋ–Η–Η ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Ι –€–Α–Κ―¹–≤–Β–Μ–Μ–Α –¥–Μ―è ―¹–Μ―É―΅–Α―è ―Ä–Α―¹–Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ–Β–Ϋ–Η―è –≤–Ψ–Μ–Ϋ―΄ –≤ –Ω―Ä–Ψ–≤–Ψ–¥―è―â–Β–Ι ―¹―Ä–Β–¥–Β (–Ω–Μ–Α–Ζ–Φ–Β) –Ψ–Κ–Α–Ζ―΄–≤–Α–Β―²―¹―è ―É–¥–Ψ–±–Ϋ―΄–Φ –≤–≤–Β―¹―²–Η –Κ–Ψ–Φ–Ω–Μ–Β–Κ―¹–Ϋ―É―é –¥–Η―ç–Μ–Β–Κ―²―Ä–Η―΅–Β―¹–Κ―É―é –Ω―Ä–Ψ–Ϋ–Η―Ü–Α–Β–Φ–Ψ―¹―²―¨ ―¹―Ä–Β–¥―΄ –≤ –≤–Η–¥–Β: –ö–Ψ–Φ–Ω–Μ–Β–Κ―¹–Ϋ–Α―è –¥–Η―ç–Μ–Β–Κ―²―Ä–Η―΅–Β―¹–Κ–Α―è –Ω―Ä–Ψ–Ϋ–Η―Ü–Α–Β–Φ–Ψ―¹―²―¨ (2.3) ―Ä–Α–≤–Ϋ–Α –Κ–≤–Α–¥―Ä–Α―²―É –Κ–Ψ–Φ–Ω–Μ–Β–Κ―¹–Ϋ–Ψ–≥–Ψ –Ω–Ψ–Κ–Α–Ζ–Α―²–Β–Μ―è –Ω―Ä–Β–Μ–Ψ–Φ–Μ–Β–Ϋ–Η―è, –Κ–Ψ―²–Ψ―Ä―΄–Ι, –≤ ―¹–≤–Ψ―é –Ψ―΅–Β―Ä–Β–¥―¨, ―¹–Ψ―¹―²–Ψ–Η―² –Η–Ζ –Ψ–±―΄―΅–Ϋ–Ψ–≥–Ψ –Ω–Ψ–Κ–Α–Ζ–Α―²–Β–Μ―è –Ω―Ä–Β–Μ–Ψ–Φ–Μ–Β–Ϋ–Η―è n (–¥–Β–Ι―¹―²–≤–Η―²–Β–Μ―¨–Ϋ–Α―è ―΅–Α―¹―²―¨) –Η –Κ–Ψ―ç―³―³–Η―Ü–Η–Β–Ϋ―²–Α –Ω–Ψ–≥–Μ–Ψ―â–Β–Ϋ–Η―è k (–Φ–Ϋ–Η–Φ–Α―è ―΅–Α―¹―²―¨). –£–Ϋ–Α―΅–Α–Μ–Β ―Ä–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―¹–Μ―É―΅–Α–Ι –±–Β–Ζ –Φ–Α–≥–Ϋ–Η―²–Ϋ–Ψ–≥–Ψ –Ω–Ψ–Μ―è (). –‰–Ζ ―Ä–Β―à–Β–Ϋ–Η―è ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η―è –¥–≤–Η–Ε–Β–Ϋ–Η―è –¥–Μ―è ―ç–Μ–Β–Κ―²―Ä–Ψ–Ϋ–Α (2.1) –Φ–Ψ–Ε–Ϋ–Ψ –Ϋ–Α–Ι―²–Η: –£―΄―Ä–Α–Ε–Β–Ϋ–Η–Β –¥–Μ―è ―΅–Α―¹―²–Ψ―²―΄ ―¹―²–Ψ–Μ–Κ–Ϋ–Ψ–≤–Β–Ϋ–Η–Ι n―¹―² –Ψ–Ω―Ä–Β–¥–Β–Μ―è–Β―²―¹―è ―Ä–Β―à–Β–Ϋ–Η–Β–Φ –Ζ–Α–¥–Α―΅–Η –Ψ ―Ä–Α―¹―¹–Β―è–Ϋ–Η–Η: –≥–¥–Β βÄ™ ―¹―Ä–Β–¥–Ϋ―è―è ―¹–Κ–Ψ―Ä–Ψ―¹―²―¨ ―ç–Μ–Β–Κ―²―Ä–Ψ–Ϋ–Ψ–≤, –Α N βÄî –Η―Ö –Κ–Ψ–Ϋ―Ü–Β–Ϋ―²―Ä–Α―Ü–Η―è. –£ ―É―¹–Μ–Ψ–≤–Η―è―Ö ―¹–Ψ–Μ–Ϋ–Β―΅–Ϋ–Ψ–Ι –Κ–Ψ―Ä–Ψ–Ϋ―΄ (N ~ 108 ―¹–ΦβÄ™3) n―¹―² ~ 1/15 ―¹βÄ™1 << w –¥–Μ―è –≤―¹–Β–≥–Ψ –¥–Η–Α–Ω–Α–Ζ–Ψ–Ϋ–Α ―Ä–Α–¥–Η–Ψ–≤–Ψ–Μ–Ϋ, –Ω–Ψ―ç―²–Ψ–Φ―É w2 + n―¹―²2 @ w2. –î–Μ―è –≤–Ψ–Μ–Ϋ―΄, ―Ä–Α―¹–Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―è―é―â–Β–Ι―¹―è –≤–¥–Ψ–Μ―¨ –Ψ―¹–Η z –≤ –Ω–Μ–Α–Ζ–Φ–Β ―¹ –¥–Η―ç–Μ–Β–Κ―²―Ä–Η―΅–Β―¹–Κ–Ψ–Ι –Ω―Ä–Ψ–Ϋ–Η―Ü–Α–Β–Φ–Ψ―¹―²―¨―é e¢ (2.3), ―Ä–Β―à–Β–Ϋ–Η–Β ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Ι –€–Α–Κ―¹–≤–Β–Μ–Μ–Α –¥–Α–Β―²: –£―΄–±–Η―Ä–Α–Β–Φ –≤–Β―Ä―Ö–Ϋ–Η–Β –Ζ–Ϋ–Α–Κ–Η –≤ ―ç–Κ―¹–Ω–Ψ–Ϋ–Β–Ϋ―²–Β –Η–Ζ ―¹–Ψ–Ψ–±―Ä–Α–Ε–Β–Ϋ–Η–Ι –Η―¹―΅–Β–Ζ–Ϋ–Ψ–≤–Β–Ϋ–Η―è –≤–Ψ–Μ–Ϋ―΄ –Ϋ–Α –±–Β―¹–Κ–Ψ–Ϋ–Β―΅–Ϋ–Ψ―¹―²–Η. –ü–Β―Ä–≤–Ψ–Β ―¹–Μ–Α–≥–Α–Β–Φ–Ψ–Β –≤ –Ω–Ψ–Κ–Α–Ζ–Α―²–Β–Μ–Β ―ç–Κ―¹–Ω–Ψ–Ϋ–Β–Ϋ―²―΄ ―Ö–Α―Ä–Α–Κ―²–Β―Ä–Η–Ζ―É–Β―² ―Ä–Α―¹–Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ–Β–Ϋ–Η–Β –≤–Ψ–Μ–Ϋ―΄ –≤ ―¹―Ä–Β–¥–Β ―¹ –Ω–Ψ–Κ–Α–Ζ–Α―²–Β–Μ–Β–Φ –Ω―Ä–Β–Μ–Ψ–Φ–Μ–Β–Ϋ–Η―è –Ϋ–Α–Ζ―΄–≤–Α–Β―²―¹―è –Ω–Μ–Α–Ζ–Φ–Β–Ϋ–Ϋ–Ψ–Ι (–Μ–Β–Ϋ–≥–Φ―é―Ä–Ψ–≤―¹–Κ–Ψ–Ι) ―΅–Α―¹―²–Ψ―²–Ψ–Ι –Η ―Ö–Α―Ä–Α–Κ―²–Β―Ä–Η–Ζ―É–Β―² ―΅–Α―¹―²–Ψ―²―É ―¹–Ψ–±―¹―²–≤–Β–Ϋ–Ϋ―΄―Ö –Κ–Ψ–Μ–Β–±–Α–Ϋ–Η–Ι –Ω–Μ–Α–Ζ–Φ―΄. –ü–Μ–Α–Ζ–Φ–Β–Ϋ–Ϋ–Α―è ―΅–Α―¹―²–Ψ―²–Α –Ζ–Α–≤–Η―¹–Η―² (–Ω–Ψ–Φ–Η–Φ–Ψ –Α―²–Ψ–Φ–Ϋ―΄―Ö –Κ–Ψ–Ϋ―¹―²–Α–Ϋ―²) ―²–Ψ–Μ―¨–Κ–Ψ –Ψ―² –Φ–Β―¹―²–Ϋ–Ψ–Ι ―ç–Μ–Β–Κ―²―Ä–Ψ–Ϋ–Ϋ–Ψ–Ι –Κ–Ψ–Ϋ―Ü–Β–Ϋ―²―Ä–Α―Ü–Η–Η. –ü―Ä–Η–±–Μ–Η–Ε–Β–Ϋ–Ϋ–Ψ –Δ–Α–Κ–Η–Φ –Ψ–±―Ä–Α–Ζ–Ψ–Φ, –Ω―Ä–Η w ³ wp –Κ–Ψ―ç―³―³–Η―Ü–Η–Β–Ϋ―² –Ω―Ä–Β–Μ–Ψ–Φ–Μ–Β–Ϋ–Η―è –Ω–Μ–Α–Ζ–Φ―΄ –≤―¹–Β–≥–¥–Α –Ζ–Α–Κ–Μ―é―΅–Β–Ϋ –≤ –Ω―Ä–Β–¥–Β–Μ–Α―Ö 0 £ n £ 1; –Ω―Ä–Η w < wp –Κ–Ψ―ç―³―³–Η―Ü–Η–Β–Ϋ―² –Ω―Ä–Β–Μ–Ψ–Φ–Μ–Β–Ϋ–Η―è ―¹―²–Α–Ϋ–Ψ–≤–Η―²―¹―è –Φ–Ϋ–Η–Φ―΄–Φ. –≠―²–Ψ –Ψ–Ζ–Ϋ–Α―΅–Α–Β―², ―΅―²–Ψ –≤ –Α–Φ–Ω–Μ–Η―²―É–¥–Β –≤–Ψ–Μ–Ϋ―΄ –Ω–Ψ―è–≤–Η―²―¹―è –Β―â–Β –Ψ–¥–Η–Ϋ ―ç–Κ―¹–Ω–Ψ–Ϋ–Β–Ϋ―Ü–Η–Α–Μ―¨–Ϋ–Ψ –Ζ–Α―²―É―Ö–Α―é―â–Η–Ι –Φ–Ϋ–Ψ–Ε–Η―²–Β–Μ―¨, –Η –≤–Ψ–Μ–Ϋ–Α –±―É–¥–Β―² –Ω–Ψ–≥–Μ–Ψ―â–Β–Ϋ–Α –Ϋ–Α ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Η ~l. –£–Ψ–Μ–Ϋ―΄ ―¹ w < wp –≤ –Ω–Μ–Α–Ζ–Φ–Β ―Ä–Α―¹–Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―è―²―¨―¹―è –Ϋ–Β –Φ–Ψ–≥―É―². –£–Β–Μ–Η―΅–Η–Ϋ–Α ¬†–≤ –Ω–Ψ–Κ–Α–Ζ–Α―²–Β–Μ–Β ―ç–Κ―¹–Ω–Ψ–Ϋ–Β–Ϋ―²―΄ –≤ (2.6) ―Ö–Α―Ä–Α–Κ―²–Β―Ä–Η–Ζ―É–Β―² ―É–Φ–Β–Ϋ―¨―à–Β–Ϋ–Η–Β –Α–Φ–Ω–Μ–Η―²―É–¥―΄ –≤–Ψ–Μ–Ϋ―΄ –Ζ–Α ―¹―΅–Β―² –Ω–Ψ–≥–Μ–Ψ―â–Β–Ϋ–Η―è –≤ –Ω–Μ–Α–Ζ–Φ–Β –Ω―Ä–Η ―¹–≤–Ψ–±–Ψ–¥–Ϋ–Ψ-―¹–≤–Ψ–±–Ψ–¥–Ϋ―΄―Ö –Ω–Β―Ä–Β―Ö–Ψ–¥–Α―Ö. –ß―²–Ψ–±―΄ –Ω–Β―Ä–Β–Ι―²–Η –Κ –±–Ψ–Μ–Β–Β –Ω―Ä–Η–≤―΄―΅–Ϋ–Ψ–Φ―É –Κ–Ψ―ç―³―³–Η―Ü–Η–Β–Ϋ―²―É –Ω–Ψ–≥–Μ–Ψ―â–Β–Ϋ–Η―è –¥–Μ―è –Η–Ϋ―²–Β–Ϋ―¹–Η–≤–Ϋ–Ψ―¹―²–Η, –Ϋ–Β–Ψ–±―Ö–Ψ–¥–Η–Φ–Ψ –≤–Ζ―è―²―¨ –Κ–≤–Α–¥―Ä–Α―² –Φ–Ψ–¥―É–Μ―è –Κ–Ψ–Φ–Ω–Μ–Β–Κ―¹–Ϋ–Ψ–Ι –Α–Φ–Ω–Μ–Η―²―É–¥―΄ ―ç–Μ–Β–Κ―²―Ä–Η―΅–Β―¹–Κ–Ψ–≥–Ψ –Ω–Ψ–Μ―è, ―²–Ψ–≥–¥–Α –Κ–Ψ―ç―³―³–Η―Ü–Η–Β–Ϋ―² –Ω–Ψ–≥–Μ–Ψ―â–Β–Ϋ–Η―è ―É–¥–≤–Α–Η–≤–Α–Β―²―¹―è, –Η –Ω–Ψ–Μ―É―΅–Η–Φ: –†–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ ―Ä–Α―¹–Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ–Β–Ϋ–Η–Β ―ç–Μ–Β–Κ―²―Ä–Ψ–Φ–Α–≥–Ϋ–Η―²–Ϋ–Ψ–Ι –≤–Ψ–Μ–Ϋ―΄ –≤ –Ω–Μ–Α–Ζ–Φ–Β ―¹ –Φ–Α–≥–Ϋ–Η―²–Ϋ―΄–Φ –Ω–Ψ–Μ–Β–Φ. –£ –Ζ–Α–Φ–Α–≥–Ϋ–Η―΅–Β–Ϋ–Ϋ–Ψ–Ι –Ω–Μ–Α–Ζ–Φ–Β, –Κ―Ä–Ψ–Φ–Β –Μ–Β–Ϋ–≥–Φ―é―Ä–Ψ–≤―¹–Κ–Ψ–Ι ―΅–Α―¹―²–Ψ―²―΄, –≤–Ψ–Ζ–Ϋ–Η–Κ–Α–Β―² –Β―â–Β –Ψ–¥–Ϋ–Α –Ψ―¹–Ψ–±–Α―è ―΅–Α―¹―²–Ψ―²–Α βÄ™ –≥–Η―Ä–Ψ―΅–Α―¹―²–Ψ―²–Α –Λ–Ψ―Ä–Φ―É–Μ–Α –¥–Μ―è –Ω―Ä–Η–±–Μ–Η–Ε–Β–Ϋ–Ϋ―΄―Ö –Ψ―Ü–Β–Ϋ–Ψ–Κ: –‰―¹–Ω–Ψ–Μ―¨–Ζ―É–Β–Φ –Ω―Ä–Η–±–Μ–Η–Ε–Β–Ϋ–Η–Β , ―΅―²–Ψ –≤―¹–Β–≥–¥–Α –≤―΄–Ω–Ψ–Μ–Ϋ―è–Β―²―¹―è –≤ –±–Ψ–Μ―¨―à–Η–Ϋ―¹―²–≤–Β –Α―¹―²―Ä–Ψ―³–Η–Ζ–Η―΅–Β―¹–Κ–Η―Ö –Ψ–±―ä–Β–Κ―²–Ψ–≤ (–≤ ―²–Ψ–Φ ―΅–Η―¹–Μ–Β –≤ –Κ–Ψ―Ä–Ψ–Ϋ–Β –Γ–Ψ–Μ–Ϋ―Ü–Α), –Ϋ–Ψ –Φ–Ψ–Ε–Β―² –Ϋ–Α―Ä―É―à–Α―²―¨―¹―è –≤ –Α–Κ―²–Η–≤–Ϋ―΄―Ö –Ψ–±–Μ–Α―¹―²―è―Ö –Ϋ–Α –Γ–Ψ–Μ–Ϋ―Ü–Β, –≥–¥–Β –Φ–Α–≥–Ϋ–Η―²–Ϋ―΄–Β –Ω–Ψ–Μ―è –¥–Ψ―¹―²–Η–≥–Α―é―² ―¹–Ψ―²–Β–Ϋ –Η ―²―΄―¹―è―΅ –™–Α―É―¹―¹. –£ –Ω–Μ–Α–Ζ–Φ–Β –Φ–Α–≥–Ϋ–Η―²–Ϋ–Ψ–Β –Ω–Ψ–Μ–Β ―¹–Ψ–Ζ–¥–Α–Β―² –≤―΄–¥–Β–Μ–Β–Ϋ–Ϋ–Ψ–Β –Ϋ–Α–Ω―Ä–Α–≤–Μ–Β–Ϋ–Η–Β, –Η ―ç–Μ–Β–Κ―²―Ä–Η―΅–Β―¹–Κ–Η–Β ―¹–≤–Ψ–Ι―¹―²–≤–Α –Ω–Μ–Α–Ζ–Φ―΄ –Ψ–Κ–Α–Ζ―΄–≤–Α―é―²―¹―è –Ϋ–Β–Ψ–¥–Η–Ϋ–Α–Κ–Ψ–≤―΄–Φ–Η –≤–¥–Ψ–Μ―¨ –Η –Ω–Ψ–Ω–Β―Ä–Β–Κ –Ω–Ψ–Μ―è. –£ ―ç―²–Ψ–Φ ―¹–Φ―΄―¹–Μ–Β –Ω–Μ–Α–Ζ–Φ―É –Φ–Ψ–Ε–Ϋ–Ψ ―É–Ω–Ψ–¥–Ψ–±–Η―²―¨ –Κ―Ä–Η―¹―²–Α–Μ–Μ―É ―¹ –¥–≤―É–Μ―É―΅–Β–Ω―Ä–Β–Μ–Ψ–Φ–Μ–Β–Ϋ–Η–Β–Φ, ―É –Κ–Ψ―²–Ψ―Ä–Ψ–≥–Ψ –Ω–Ψ–Κ–Α–Ζ–Α―²–Β–Μ–Η –Ω―Ä–Β–Μ–Ψ–Φ–Μ–Β–Ϋ–Η―è ―Ä–Α–Ζ–Μ–Η―΅–Ϋ―΄ –¥–Μ―è ―¹–≤–Β―²–Α, ―Ä–Α―¹–Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―è―é―â–Β–≥–Ψ―¹―è –≤–¥–Ψ–Μ―¨ –Η–Μ–Η –Ω–Ψ–Ω–Β―Ä–Β–Κ –Ψ–Ω―²–Η―΅–Β―¹–Κ–Ψ–Ι –Ψ―¹–Η. –Δ–Α–Κ –Ε–Β, –Κ–Α–Κ –≤ –Κ―Ä–Η―¹―²–Α–Μ–Μ–Β, –Ω―Ä–Ψ–Η–Ζ–Ψ–Ι–¥–Β―² ―Ä–Α–Ζ–¥–Β–Μ–Β–Ϋ–Η–Β –Η―¹―Ö–Ψ–¥–Ϋ–Ψ–Ι –≤–Ψ–Μ–Ϋ―΄ –Ϋ–Α –¥–≤–Β –≤–Ψ–Μ–Ϋ―΄ (–Ψ–±―΄–Κ–Ϋ–Ψ–≤–Β–Ϋ–Ϋ―É―é βÄ™ 1 –Η –Ϋ–Β–Ψ–±―΄–Κ–Ϋ–Ψ–≤–Β–Ϋ–Ϋ―É―é βÄ™ 2) ―¹ ―Ä–Α–Ζ–Μ–Η―΅–Ϋ―΄–Φ–Η –Ϋ–Α–Ω―Ä–Α–≤–Μ–Β–Ϋ–Η―è–Φ–Η –Ω–Ψ–Μ―è―Ä–Η–Ζ–Α―Ü–Η–Η. –î–Μ―è –Κ–Α–Ε–¥–Ψ–Ι –Η–Ζ –≤–Ψ–Μ–Ϋ –±―É–¥―É―² –Η–Φ–Β―²―¨ –Φ–Β―¹―²–Ψ ―Ä–Α–Ζ–Ϋ―΄–Β –Ω–Ψ–Κ–Α–Ζ–Α―²–Β–Μ–Η –Ω―Ä–Β–Μ–Ψ–Φ–Μ–Β–Ϋ–Η―è. –†–Α―¹―¹–Φ–Ψ―²―Ä–Η–Φ –¥–≤–Α ―¹–Μ―É―΅–Α―è: a = 0 –Η a = p/2 (a βÄ™ ―É–≥–Ψ–Μ –Φ–Β–Ε–¥―É –Ϋ–Α–Ω―Ä–Α–≤–Μ–Β–Ϋ–Η―è–Φ–Η –Φ–Α–≥–Ϋ–Η―²–Ϋ–Ψ–≥–Ψ –Ω–Ψ–Μ―è –Η ―Ä–Α―¹–Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ–Β–Ϋ–Η―è ―ç–Μ–Β–Κ―²―Ä–Ψ–Φ–Α–≥–Ϋ–Η―²–Ϋ–Ψ–Ι –≤–Ψ–Μ–Ϋ―΄). –û–±―â–Η–Ι ―¹–Μ―É―΅–Α–Ι ―¹–Μ–Ψ–Ε–Β–Ϋ, –Ω–Ψ–¥―Ä–Ψ–±–Ϋ–Ψ―¹―²–Η –Φ–Ψ–Ε–Ϋ–Ψ –Ϋ–Α–Ι―²–Η –≤ –Κ–Ϋ–Η–≥–Β –£.–¦. –™–Η–Ϋ–Ζ–±―É―Ä–≥–Α [16]. 1) a = 0 (–Ω―Ä–Ψ–¥–Ψ–Μ―¨–Ϋ–Ψ–Β ―Ä–Α―¹–Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ–Β–Ϋ–Η–Β). –£–Ψ–Μ–Ϋ–Α ―Ä–Α―¹–Ω–Α–¥–Α–Β―²―¹―è –Ϋ–Α –¥–≤–Β –Ω–Ψ–Μ―è―Ä–Η–Ζ–Ψ–≤–Α–Ϋ–Ϋ―΄–Β –Ω–Ψ –Κ―Ä―É–≥―É –≤–Ψ–Μ–Ϋ―΄. –½–Ϋ–Α–Κ–Η + –Ψ―²–Ϋ–Ψ―¹―è―²―¹―è –Κ –Η–Ϋ–¥–Β–Κ―¹―É 1 (–Ψ–±―΄–Κ–Ϋ–Ψ–≤–Β–Ϋ–Ϋ–Α―è –≤–Ψ–Μ–Ϋ–Α), –Ζ–Ϋ–Α–Κ–Η βÄ™ βÄ™ –Κ –Η–Ϋ–¥–Β–Κ―¹―É 2 (–Ϋ–Β–Ψ–±―΄–Κ–Ϋ–Ψ–≤–Β–Ϋ–Ϋ–Α―è –≤–Ψ–Μ–Ϋ–Α). –î–Μ―è –Ϋ–Β–Ψ–±―΄–Κ–Ϋ–Ψ–≤–Β–Ϋ–Ϋ–Ψ–Ι –≤–Ψ–Μ–Ϋ―΄ ―Ä–Β–Ζ–Κ–Ψ –≤–Ψ–Ζ―Ä–Α―¹―²–Α–Β―² –Κ–Ψ―ç―³―³–Η―Ü–Η–Β–Ϋ―² –Ω–Ψ–≥–Μ–Ψ―â–Β–Ϋ–Η―è –≤–±–Μ–Η–Ζ–Η w ~ wH; –Ω–Ψ―ç―²–Ψ–Φ―É –Ϋ–Α ―΅–Α―¹―²–Ψ―²–Α―Ö –≤–±–Μ–Η–Ζ–Η –≥–Η―Ä–Ψ―΅–Α―¹―²–Ψ―²―΄ –Ω–Β―Ä–≤–Ψ–Ϋ–Α―΅–Α–Μ―¨–Ϋ–Ψ –Ϋ–Β–Ω–Ψ–Μ―è―Ä–Η–Ζ–Ψ–≤–Α–Ϋ–Ϋ–Ψ–Β –Η–Ζ–Μ―É―΅–Β–Ϋ–Η–Β –Φ–Ψ–Ε–Β―² –Ω―Ä–Η–Ψ–±―Ä–Β―¹―²–Η –Κ―Ä―É–≥–Ψ–≤―É―é –Ω–Ψ–Μ―è―Ä–Η–Ζ–Α―Ü–Η―é. –Θ –Ϋ–Β–Ψ–±―΄–Κ–Ϋ–Ψ–≤–Β–Ϋ–Ϋ–Ψ–Ι –≤–Ψ–Μ–Ϋ―΄ –Ϋ–Α–Ω―Ä–Α–≤–Μ–Β–Ϋ–Η–Β –Κ―Ä―É–≥–Ψ–≤–Ψ–Ι –Ω–Ψ–Μ―è―Ä–Η–Ζ–Α―Ü–Η–Η ―¹–Ψ–≤–Ω–Α–¥–Α–Β―² ―¹ –Ϋ–Α–Ω―Ä–Α–≤–Μ–Β–Ϋ–Η–Β–Φ –Μ–Α―Ä–Φ–Ψ―Ä–Ψ–≤―¹–Κ–Ψ–≥–Ψ –≤―Ä–Α―â–Β–Ϋ–Η―è ―ç–Μ–Β–Κ―²―Ä–Ψ–Ϋ–Ψ–≤ –≤–Ψ–Κ―Ä―É–≥ –Φ–Α–≥–Ϋ–Η―²–Ϋ―΄―Ö ―¹–Η–Μ–Ψ–≤―΄―Ö –Μ–Η–Ϋ–Η–Ι, –Ω–Ψ―ç―²–Ψ–Φ―É –≤–Ψ–Μ–Ϋ–Α –Η―¹–Ω―΄―²―΄–≤–Α–Β―² –Ω–Ψ–≤―΄―à–Β–Ϋ–Ϋ―΄–Β –Ω–Ψ―²–Β―Ä–Η ―ç–Ϋ–Β―Ä–≥–Η–Η –Ω–Ψ ―¹―Ä–Α–≤–Ϋ–Β–Ϋ–Η―é ―¹ –Ψ–±―΄–Κ–Ϋ–Ψ–≤–Β–Ϋ–Ϋ–Ψ–Ι. 2) a = p/2 (–Ω–Ψ–Ω–Β―Ä–Β―΅–Ϋ–Ψ–Β ―Ä–Α―¹–Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ–Β–Ϋ–Η–Β). –£–Ψ–Μ–Ϋ–Α ―Ä–Α―¹–Ω–Α–¥–Α–Β―²―¹―è –Ϋ–Α –¥–≤–Β –≤–Ψ–Μ–Ϋ―΄ ―¹ –≤–Ζ–Α–Η–Φ–Ϋ–Ψ –Ψ―Ä―²–Ψ–≥–Ψ–Ϋ–Α–Μ―¨–Ϋ―΄–Φ–Η –Μ–Η–Ϋ–Β–Ι–Ϋ―΄–Φ–Η –Ω–Ψ–Μ―è―Ä–Η–Ζ–Α―Ü–Η―è–Φ–Η. –Θ –Ψ–±―΄–Κ–Ϋ–Ψ–≤–Β–Ϋ–Ϋ–Ψ–Ι –≤–Ψ–Μ–Ϋ―΄ –≤–Β–Κ―²–Ψ―Ä ―ç–Μ–Β–Κ―²―Ä–Η―΅–Β―¹–Κ–Ψ–≥–Ψ –Ω–Ψ–Μ―è βÄ™ –≤–Β–Κ―²–Ψ―Ä―É –Φ–Α–≥–Ϋ–Η―²–Ϋ–Ψ–≥–Ψ –Ω–Ψ–Μ―è, –Η –Φ–Α–≥–Ϋ–Η―²–Ϋ–Ψ–Β –Ω–Ψ–Μ–Β –Ϋ–Β –Ψ–Κ–Α–Ζ―΄–≤–Α–Β―² –≤–Μ–Η―è–Ϋ–Η―è –Ϋ–Α –¥–≤–Η–Ε–Β–Ϋ–Η―è ―ç–Μ–Β–Κ―²―Ä–Ψ–Ϋ–Ψ–≤. –ü–Ψ―ç―²–Ψ–Φ―É –¥–Μ―è –Ψ–±―΄–Κ–Ϋ–Ψ–≤–Β–Ϋ–Ϋ–Ψ–Ι –≤–Ψ–Μ–Ϋ―΄ n1 –Η k1 ―¹–Ψ–≤–Ω–Α–¥–Α―é―² ―¹ –≤―΄―Ä–Α–Ε–Β–Ϋ–Η―è–Φ–Η (2.13) –¥–Μ―è ―¹–Μ―É―΅–Α―è . –î–Μ―è –Ϋ–Β–Ψ–±―΄–Κ–Ϋ–Ψ–≤–Β–Ϋ–Ϋ–Ψ–Ι –≤–Ψ–Μ–Ϋ―΄: –£ ―¹–Μ―É―΅–Α–Β –Ω–Ψ–Ω–Β―Ä–Β―΅–Ϋ–Ψ–≥–Ψ ―Ä–Α―¹–Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ–Β–Ϋ–Η―è, –Η–Ζ-–Ζ–Α –Ω–Ψ–≤―΄―à–Β–Ϋ–Ϋ–Ψ–≥–Ψ –Ω–Ψ–≥–Μ–Ψ―â–Β–Ϋ–Η―è –Ϋ–Β–Ψ–±―΄–Κ–Ϋ–Ψ–≤–Β–Ϋ–Ϋ–Ψ–Ι –≤–Ψ–Μ–Ϋ―΄ –≤–±–Μ–Η–Ζ–Η ―΅–Α―¹―²–Ψ―²―΄ ¬†–Φ–Ψ–Ε–Β―² –≤–Ψ–Ζ–Ϋ–Η–Κ–Ϋ―É―²―¨ –Μ–Η–Ϋ–Β–Ι–Ϋ–Α―è –Ω–Ψ–Μ―è―Ä–Η–Ζ–Α―Ü–Η―è –Ω–Β―Ä–≤–Ψ–Ϋ–Α―΅–Α–Μ―¨–Ϋ–Ψ –Ϋ–Β –Ω–Ψ–Μ―è―Ä–Η–Ζ–Ψ–≤–Α–Ϋ–Ϋ–Ψ–≥–Ψ –Η–Ζ–Μ―É―΅–Β–Ϋ–Η―è. |
| –ß–Η―²–Α–Ι―²–Β: |
|---|