| –î―Ä―É–≥–Η–Β –Η–Ζ–Φ–Β―Ä–Β–Ϋ–Η―è? |
| –ö–Ψ―¹–Φ–Ψ–Μ–Ψ–≥–Η―è - –ù–Α―à–Α –Κ–Ψ―¹–Φ–Η―΅–Β―¹–Κ–Α―è –Ψ–±–Η―²–Β–Μ―¨ |
|
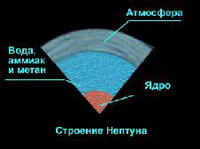
–£―¹–Β–Μ–Β–Ϋ–Ϋ―΄–Β –Φ–Ψ–≥―É―² –Ε–Η―²―¨ –Ϋ–Β–¥–Ψ–Μ–≥–Ψ, –Ω–Ψ–¥―΅–Η–Ϋ―è―²―¨―¹―è –Ψ―¹–Ϋ–Ψ–≤–Ϋ―΄–Φ ―¹–Η–Μ–Α–Φ ―Ä–Α–Ζ–Μ–Η―΅–Ϋ–Ψ–Ι –Φ–Ψ―â–Ϋ–Ψ―¹―²–Η –Η –¥–Α–Ε–Β ―¹–Κ―Ä―΄–≤–Α―²―¨ –≤ ―¹–Β–±–Β ―Ä–Α–Ζ–Ϋ–Ψ–Ψ–±―Ä–Α–Ζ–Ϋ―΄–Ι ¬Ϊ–Ζ–Ψ–Ψ–Ω–Α―Ä–Κ¬Μ ―³―É–Ϋ–¥–Α–Φ–Β–Ϋ―²–Α–Μ―¨–Ϋ―΄―Ö ―΅–Α―¹―²–Η―Ü. –ù–Ψ –Φ–Ψ–Ε–Β―² –Μ–Η –Κ–Ψ–Μ–Η―΅–Β―¹―²–≤–Ψ –Η―Ö –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Β–Ϋ–Ϋ―΄―Ö –Η–Ζ–Φ–Β―Ä–Β–Ϋ–Η–Ι –Ψ―²–Μ–Η―΅–Α―²―¨―¹―è –Ψ―² –Ϋ–Α―à–Η―Ö ―²―Ä–Β―Ö? –Δ–Α–Κ–Η–Β –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Α –Ψ–±―΄―΅–Ϋ―΄ –¥–Μ―è –Φ–Α―²–Β–Φ–Α―²–Η–Κ–Η, –Ϋ–Ψ –Ψ―Ö–≤–Α―²–Η―²―¨ –Η―Ö ―³–Η–Ζ–Η–Κ―É –≥–Ψ―Ä–Α–Ζ–¥–Ψ ―¹–Μ–Ψ–Ε–Ϋ–Β–Β. –£ –¥–≤―É―Ö–Φ–Β―Ä–Ϋ–Ψ–Φ –Φ–Η―Ä–Β –Ϋ–Β–≤–Ψ–Ζ–Φ–Ψ–Ε–Ϋ–Ψ ―¹–Ψ–Ζ–¥–Α―²―¨ ―¹–Μ–Ψ–Ε–Ϋ―΄–Β ―ç–Μ–Β–Κ―²―Ä–Η¬≠―΅–Β―¹–Κ–Η–Β ―Ü–Β–Ω–Η ―²–Α–Κ, ―΅―²–Ψ–±―΄ –Ω―Ä–Ψ–≤–Ψ–Μ–Ψ–Κ–Η, –Η―Ö ―¹–Ψ―¹―²–Α–≤–Μ―è―é―â–Η–Β, –Ϋ–Β –Ω–Β―Ä–Β―¹–Β–Κ–Α–Μ–Η―¹―¨ –¥―Ä―É–≥ ―¹ –¥―Ä―É–≥–Ψ–Φ, ―Ö–Ψ―²―è ―ç―²–Ψ –Η –Ϋ–Β –Η―¹–Κ–Μ―é―΅–Α–Β―² –Ζ–Α–Φ―΄―¹¬≠–Μ–Ψ–≤–Α―²―΄―Ö –Φ–Ψ–¥–Β–Μ–Β–Ι –≤–Ψ–Μ–Ϋ, –Κ–Ψ―²–Ψ―Ä―΄–Β –Φ–Ψ–≥―É―² –Ω―Ä–Ψ–Ϋ–Η–Ζ―΄–≤–Α―²―¨ –¥―Ä―É–≥ –¥―Ä―É–≥–Α. –î–Α–Ε–Β –≤ –Ψ–¥–Ϋ–Ψ–Φ –Η–Ζ–Φ–Β―Ä–Β–Ϋ–Η–Η –Φ–Ψ–Ε–Β―² ―¹―É―â–Β―¹―²–≤–Ψ–≤–Α―²―¨ –Ζ–Α–Ω―É―²–Α–Ϋ–Ϋ–Α―è ―¹–Μ–Ψ–Ε–Ϋ–Ψ―¹―²―¨. –£ ―¹–≤–Ψ–Β–Φ –Κ–Μ–Α―¹―¹–Η―΅–Β―¹–Κ–Ψ–Φ –Ϋ–Α―É―΅–Ϋ–Ψ-―³–Α–Ϋ―²–Α―¹―²–Η―΅–Β―¹–Κ–Ψ–Φ ―Ä–Ψ–Φ–Α–Ϋ–Β ¬Ϊ–Γ–Ψ–Ζ–¥–Α―²–Β–Μ―¨ –Ζ–≤–Β–Ζ–¥¬Μ –û–Μ–Α―³ –Γ―²–Β–Ω–Μ–¥–Ψ–Ϋ –Ψ–Ω–Η―¹―΄–≤–Α–Β―², ―¹―Ä–Β–¥–Η –Φ–Ϋ–Ψ–≥–Ψ―΅–Η―¹–Μ–Β–Ϋ–Ϋ―΄―Ö –≤–Ψ–Ψ–±―Ä–Α–Ε–Α–Β–Φ―΄―Ö –Κ–Ψ―¹–Φ–Ψ―¹–Ψ–≤, ¬Ϊ–Φ―É–Ζ―΄–Κ–Α–Μ―¨–Ϋ―É―é –£―¹–Β–Μ–Β–Ϋ–Ϋ―É―é, –≥–¥–Β ―¹–Ψ–Ζ–¥–Α–Ϋ–Η―è –Ω―Ä–Β–¥―¹―²–Α–≤–Μ―è―é―²―¹―è –¥―Ä―É–≥ –¥―Ä―É–≥―É ―¹–Μ–Ψ–Ε–Ϋ―΄–Φ–Η –≥–Α–Φ–Φ–Α–Φ–Η –Η ―Ä–Η―²–Φ–Α–Φ–Η ―²–Ψ–Ϋ–Α–Μ―¨–Ϋ–Ψ–≥–Ψ ―Ö–Α―Ä–Α–Κ―²–Β―Ä–Α. –Δ–Β–Μ–Ψ ―¹–Ψ–Ζ–¥–Α–Ϋ–Η―è –±―΄–Μ–Ψ –±–Ψ–Μ–Β–Β –Η–Μ–Η –Φ–Β–Ϋ–Β–Β –Ω–Ψ―¹―²–Ψ―è–Ϋ–Ϋ–Ψ–Ι ―²–Ψ–Ϋ–Α–Μ―¨–Ϋ–Ψ–Ι –≥–Α–Φ–Φ–Ψ–Ι, –Κ–Ψ―²–Ψ―Ä–Α―è –Φ–Ψ–≥–Μ–Α –Ω–Β―Ä–Β―¹–Β–Κ–Α―²―¨ –¥―Ä―É–≥–Η–Β –Ε–Η–≤―΄–Β ―²–Β–Μ–Α ―²–Ψ–Ι –Ε–Β –≤―΄―¹–Ψ―²―΄, –Ω–Ψ–¥–Ψ–±–Ϋ–Ψ ―²–Ψ–Φ―É, –Κ–Α–Κ ―Ü―É–≥–Η –≤–Ψ–Μ–Ϋ –≤ –Ω―Ä―É–¥―É –Ω―Ä–Ψ―Ö–Ψ–¥―è―² –Ψ–¥–Ϋ–Α ―¹–Κ–≤–Ψ–Ζ―¨ –¥―Ä―É–≥―É―é¬Μ. –€―É–Ζ―΄–Κ–Α–Μ―¨–Ϋ–Α―è –£―¹–Β–Μ–Β–Ϋ–Ϋ–Α―è –Γ―²–Β–Ω–Μ–¥–Ψ–Ϋ–Α, –Ω–Ψ–Φ–Η–Φ–Ψ –≤―Ä–Β–Φ–Β–Ϋ–Η, –Ψ–±–Μ–Α–¥–Α–Β―², –Ω–Ψ ―¹―É―²–Η, –Ψ–¥–Ϋ–Η–Φ –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Β–Ϋ–Ϋ―΄–Φ –Η–Ζ–Φ–Β―Ä–Β–Ϋ–Η–Β–Φ. –ù–Α―à–Β ―Ä–Β–Α–Μ―¨–Ϋ–Ψ–Β –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Ψ-–≤―Ä–Β–Φ―è –Η–Φ–Β–Β―², –Κ–Ψ–Ϋ–Β―΅–Ϋ–Ψ –Ε–Β, ―²―Ä–Η –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Β–Ϋ–Ϋ―΄―Ö –Η–Ζ–Φ–Β―Ä–Β–Ϋ–Η―è. –£―Ä–Β–Φ―è, ―΅–Β―²–≤–Β―Ä―²–Ψ–Β, –Ψ―²–Μ–Η―΅–Α–Β―²¬≠―¹―è –Ψ―² –Ϋ–Η―Ö ―²–Β–Φ, ―΅―²–Ψ –Η–Φ–Β–Β―² ―¹―²―Ä–Β–Μ―É: –Κ–Α–Ε–Β―²―¹―è, ―΅―²–Ψ –Φ―΄ ―²–Α―â–Η–Φ―¹―è –≤ –Ϋ–Β–Φ –≤ –Ψ–¥–Ϋ–Ψ–Φ –Ϋ–Α–Ω―Ä–Α–≤–Μ–Β–Ϋ–Η–Η (–≤–Ω–Β―Ä–Β–¥). –Θ ―²―Ä–Β―Ö–Φ–Β―Ä–Ϋ–Ψ–≥–Ψ –Ω―Ä–Ψ¬≠―¹―²―Ä–Α–Ϋ―¹―²–≤–Α –Β―¹―²―¨ –Ψ―¹–Ψ–±―΄–Β ―΅–Β―Ä―²―΄. –ö –Ω―Ä–Η–Φ–Β―Ä―É, –Β―¹–Μ–Η –Ψ–±―ä–Β–Κ―² –≤―Ä–Α¬≠―â–Α–Β―²―¹―è –Ω―Ä–Ψ–Η–Ζ–≤–Ψ–Μ―¨–Ϋ–Ψ, ―²–Ψ –¥–Μ―è –Ψ–Ω―Ä–Β–¥–Β–Μ–Β–Ϋ–Η―è –≤―Ä–Α―â–Β–Ϋ–Η―è –Ϋ–Β–Ψ–±―Ö–Ψ¬≠–¥–Η–Φ―΄ ―²―Ä–Η –≤–Β–Μ–Η―΅–Η–Ϋ―΄ βÄî –Ω–Ψ –Κ–Ψ–Μ–Η―΅–Β―¹―²–≤―É –Η–Ζ–Φ–Β―Ä–Β–Ϋ–Η–Ι: –¥–≤–Β, ―΅―²–Ψ–±―΄ –Ψ–±–Ψ–Ζ–Ϋ–Α―΅–Η―²―¨ –Ϋ–Α–Ω―Ä–Α–≤–Μ–Β–Ϋ–Η–Β –Ψ―¹–Η –≤―Ä–Α―â–Β–Ϋ–Η―è, –Η –Β―â–Β –Ψ–¥–Ϋ–Α –¥–Μ―è –Ψ–Ω―Ä–Β–¥–Β–Μ–Β–Ϋ–Η―è ―É–≥–Μ–Α, –Ω–Ψ–¥ –Κ–Ψ―²–Ψ―Ä―΄–Φ –Ψ–Ϋ –≤―Ä–Α―â–Α–Β―²―¹―è –≤–Ψ–Κ―Ä―É–≥ ―ç―²–Ψ–Ι –Ψ―¹–Η. (–£ –¥–≤―É―Ö –Η–Ζ–Φ–Β―Ä–Β–Ϋ–Η―è―Ö –Ψ–±–Ψ―Ä–Ψ―²―΄ –Ψ–Ω―Ä–Β–¥–Β–Μ―è―é―²―¹―è –≤―¹–Β–≥–Ψ –Ψ–¥–Ϋ–Η–Φ ―΅–Η―¹–Μ–Ψ–Φ, –Α –≤ ―΅–Β―²―΄―Ä–Β―Ö–Φ–Β―Ä–Ϋ–Ψ–Φ –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Β –Ϋ–Β–Ψ–±―Ö–Ψ–¥–Η–Φ―΄ ―à–Β―¹―²―¨ –≤–Β–Μ–Η―΅–Η–Ϋ.) –Δ–Α–Κ –Ω―Ä–Ψ–Η―¹―Ö–Ψ–¥–Η―² –Ω–Ψ―²–Ψ–Φ―É, ―΅―²–Ψ –Β―¹―²―¨ ―²―Ä–Η –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Β–Ϋ¬≠–Ϋ―΄―Ö –Η–Ζ–Φ–Β―Ä–Β–Ϋ–Η―è, ―¹ –Κ–Ψ―²–Ψ―Ä―΄–Φ–Η ―ç–Μ–Β–Κ―²―Ä–Η―΅–Β―¹–Κ–Η–Β –Η –≥―Ä–Α–≤–Η―²–Α―Ü–Η–Ψ–Ϋ¬≠–Ϋ―΄–Β ―¹–Η–Μ―΄ ―¹–≤―è–Ζ–Α–Ϋ―΄ –Ζ–Α–Κ–Ψ–Ϋ–Ψ–Φ –Ψ–±―Ä–Α―²–Ϋ―΄―Ö –Κ–≤–Α–¥―Ä–Α―²–Ψ–≤. –≠―²―É –Ζ–Α–≤–Η―¹–Η–Φ–Ψ―¹―²―¨ –Ω―Ä–Ψ―â–Β –≤―¹–Β–≥–Ψ –Ψ―Ü–Β–Ϋ–Η―²―¨ ―¹ –Ω–Ψ–Φ–Ψ―â―¨―é –Κ–Ψ–Ϋ―Ü–Β–Ω―Ü–Η–Η ―¹–Η¬≠–Μ–Ψ–≤―΄―Ö –Μ–Η–Ϋ–Η–Ι –Λ–Α―Ä–Α–¥–Β―è. –û–±–Ψ–Μ–Ψ―΅–Κ–Α ―Ä–Α–¥–Η―É―¹–Α r, –Ψ–Κ―Ä―É–Ε–Α―é―â–Α―è –Φ–Α―¹―¹―É –Η–Μ–Η –Ζ–Α―Ä―è–¥, –Η–Φ–Β–Β―² –Ω–Μ–Ψ―â–Α–¥―¨, –Ω―Ä―è–Φ–Ψ –Ω―Ä–Ψ–Ω–Ψ―Ä―Ü–Η–Ψ–Ϋ–Α–Μ―¨–Ϋ―É―é r2; ―¹–Η–Μ–Α ―É–Φ–Β–Ϋ―¨―à–Α–Β―²―¹―è –Ω―Ä–Ψ–Ω–Ψ―Ä―Ü–Η–Ψ–Ϋ–Α–Μ―¨–Ϋ–Ψ 1/r2, ―²–Α–Κ –Κ–Α–Κ –Ω―Ä–Η –±ó–Μ―¨―à–Η―Ö ―Ä–Α–¥–Η―É―¹–Α―Ö ―¹–Η–Μ–Ψ–≤―΄–Β –Μ–Η–Ϋ–Η–Η ―Ä–Α―¹–Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―è―é―²―¹―è –Ϋ–Α –±ó–Μ―¨―à–Η–Β –Ω–Μ–Ψ―â–Α–¥–Η –Η –Η―Ö –¥–Β–Ι―¹―²–≤–Η–Β –Ψ―¹–Μ–Α–±–Μ―è–Β―²―¹―è. –ï―¹–Μ–Η –±―΄ ―¹―É―â–Β―¹―²–≤–Ψ–≤–Α–Μ–Ψ ―΅–Β―²–≤–Β―Ä―²–Ψ–Β –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Β–Ϋ–Ϋ–Ψ–Β –Η–Ζ–Φ–Β―Ä–Β–Ϋ–Η–Β, –Ω–Μ–Ψ¬≠―â–Α–¥―¨ ―¹―³–Β―Ä―΄ –±―΄–Μ–Α –±―΄ –Ω―Ä–Ψ–Ω–Ψ―Ä―Ü–Η–Ψ–Ϋ–Α–Μ―¨–Ϋ–Α r3, –Α –Ϋ–Β r2, –Η ―¹–Η¬≠–Μ–Α –Ω–Ψ–¥―΅–Η–Ϋ―è–Μ–Α―¹―¨ –±―΄ –Ζ–Α–Κ–Ψ–Ϋ―É –Ψ–±―Ä–Α―²–Ϋ―΄―Ö –Κ―É–±–Ψ–≤. –½–Α–Κ–Ψ–Ϋ –Ψ–±―Ä–Α―²¬≠–Ϋ―΄―Ö –Κ–≤–Α–¥―Ä–Α―²–Ψ–≤ –Η–Φ–Β–Β―² ―Ö–Α―Ä–Α–Κ―²–Β―Ä–Ϋ―É―é –Ψ―¹–Ψ–±–Β–Ϋ–Ϋ–Ψ―¹―²―¨: –Ψ–Ϋ –¥–Ψ–Ω―É―¹¬≠–Κ–Α–Β―² ―É―¹―²–Ψ–Ι―΅–Η–≤―΄–Β –Ψ―Ä–±–Η―²―΄, –≤ ―²–Ψ–Φ ―¹–Φ―΄―¹–Μ–Β, ―΅―²–Ψ –Ψ―Ä–±–Η―²–Α –Ω–Μ–Α–Ϋ–Β¬≠―²―΄ –Μ–Η―à―¨ –Ϋ–Β–Ζ–Ϋ–Α―΅–Η―²–Β–Μ―¨–Ϋ–Ψ –Η–Ζ–Φ–Β–Ϋ―è–Β―²―¹―è –Ω–Ψ–¥ –¥–Β–Ι―¹―²–≤–Η–Β–Φ ―¹–Μ–Α–±–Ψ–≥–Ψ ¬Ϊ―²–Ψ–Μ―΅–Κ–Α¬Μ (–Ϋ–Α–Ω―Ä–Η–Φ–Β―Ä, ―²–Α–Κ–Ψ–≥–Ψ, –Κ–Ψ―²–Ψ―Ä―΄–Ι –≤―΄–Ζ―΄–≤–Α–Β―² –Ψ―²–¥–Α―΅–Α –Ω–Ψ¬≠―¹–Μ–Β ―¹―²–Ψ–Μ–Κ–Ϋ–Ψ–≤–Β–Ϋ–Η―è ―¹ –Α―¹―²–Β―Ä–Ψ–Η–¥–Ψ–Φ). –£―¹–Β –±―΄–Μ–Ψ –±―΄ ―¹–Ψ–≤–Β―Ä―à–Β–Ϋ–Ϋ–Ψ –¥―Ä―É–≥–Η–Φ, –Β―¹–Μ–Η –±―΄ –≥―Ä–Α–≤–Η―²–Α―Ü–Η―è –Ω–Ψ–¥―΅–Η–Ϋ―è–Μ–Α―¹―¨ –Ζ–Α–Κ–Ψ–Ϋ―É –Ψ–±―Ä–Α―²–Ϋ―΄―Ö –Κ―É–±–Ψ–≤: –Ω–Μ–Α–Ϋ–Β―²–Α, ―¹–Μ–Β–≥–Κ–Α –Ζ–Α–Φ–Β–¥–Μ–Η–≤―à–Α―è ―Ö–Ψ–¥, –≤―Ä–Β–Ζ–Α–Μ–Α―¹―¨ –±―΄ –≤ –Γ–Ψ–Μ–Ϋ―Ü–Β; –Β―¹–Μ–Η –Ε–Β –Β–Β ―¹–Μ–Β–≥–Κ–Α ―É―¹–Κ–Ψ―Ä–Η―²―¨, –Ψ–Ϋ–Α –±―΄ –Ω–Ψ ―¹–Ω–Η―Ä–Α–Μ–Η ―É―¹―²―Ä–Β–Φ–Η–Μ–Α―¹―¨ –≤ ―Ö–Ψ–Μ–Ψ–¥–Ϋ―É―é –Φ–Β–Ε–Ζ–≤–Β–Ζ–¥–Ϋ―É―é ―²–Β–Φ–Ϋ–Ψ―²―É. –≠―²–Ψ―² –≤―΄–≤–Ψ–¥ ―²–Β–Ω–Β―Ä―¨ –Φ–Ψ–Ε–Ϋ–Ψ –Ψ―²–Ϋ–Β―¹―²–Η –Κ –Ψ―¹–Ψ–±―΄–Φ –±–Η–Ψ―³–Η–Μ–Η―΅–Ϋ―΄–Φ –Ω–Ψ―¹–Μ–Β–¥―¹―²–≤–Η¬≠―è–Φ ―²―Ä–Β―Ö –Η–Ζ–Φ–Β―Ä–Β–Ϋ–Η–Ι –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Α. –‰–Φ–Β–Ϋ–Ϋ–Ψ ―²–Β–Ψ–Μ–Ψ–≥ –≤–Ψ―¹–Β–Φ–Ϋ–Α–¥―Ü–Α―²–Ψ–≥–Ψ –≤–Β–Κ–Α –Θ–Η–Μ―¨―è–Φ –ü–Β–Ι–Μ–Η (–Ψ–Ϋ –Ζ–Ϋ–Α–Φ–Β–Ϋ–Η―² ―¹–≤–Ψ–Η–Φ–Η –Ω–Ψ–Ω―΄―²–Κ–Α–Φ–Η –¥–Ψ–Κ–Α–Ζ–Α―²―¨, ―΅―²–Ψ –¥–Μ―è ―¹–Ψ–Ζ–¥–Α–Ϋ–Η―è –£―¹–Β–Μ–Β–Ϋ–Ϋ–Ψ–Ι –Ϋ–Β–Ψ–±―Ö–Ψ–¥–Η–Φ–Ψ ―É―΅–Α―¹―²–Η–Β –Δ–≤–Ψ―Ä―Ü–Α, ―²–Α–Κ –Ε–Β, –Κ–Α–Κ –¥–Μ―è ―¹–Ψ–Ζ–¥–Α–Ϋ–Η―è ―΅–Α―¹–Ψ–≤ –Ϋ–Β–Ψ–±―Ö–Ψ–¥–Η–Φ ―΅–Α―¹–Ψ–≤―â–Η–Κ) –Ω–Β―Ä–≤―΄–Φ –Ψ―²–Φ–Β―²–Η–Μ –Ψ―¹–Ψ¬≠–±―É―é ―¹―²–Α–±–Η–Μ―¨–Ϋ–Ψ―¹―²―¨ –Ζ–Α–Κ–Ψ–Ϋ–Α –Ψ–±―Ä–Α―²–Ϋ―΄―Ö –Κ–≤–Α–¥―Ä–Α―²–Ψ–≤. (–ü–Β–Ι–Μ–Η –Ω–Ψ¬≠–Μ―É―΅–Η–Μ –Φ–Α―²–Β–Φ–Α―²–Η―΅–Β―¹–Κ–Ψ–Β –Ψ–±―Ä–Α–Ζ–Ψ–≤–Α–Ϋ–Η–Β –≤ –ö–Β–Φ–±―Ä–Η–¥–Ε–Β –≤ ―ç–Ω–Ψ―Ö―É, –Κ–Ψ–≥–¥–Α –Ϋ―¨―é―²–Ψ–Ϋ–Ψ–≤–Α –Φ–Β―Ö–Α–Ϋ–Η–Κ–Α –±―΄–Μ–Α –Ψ―¹–Ϋ–Ψ–≤–Ϋ–Ψ–Ι ―΅–Α―¹―²―¨―é ―É―΅–Β–±–Ϋ–Ψ–Ι –Ω―Ä–Ψ–≥―Ä–Α–Φ–Φ―΄.) –≠―²–Ψ –Ψ―¹–Ψ–Ζ–Ϋ–Α–Ϋ–Η–Β ―¹―²–Α–Μ–Ψ –Ψ–Ω–Ψ―Ä–Ψ–Ι –¥–Μ―è –≤―¹–Β―Ö –Β–≥–Ψ –Α―Ä–≥―ɬ≠–Φ–Β–Ϋ―²–Ψ–≤ –≤ –Ω–Ψ–Μ―¨–Ζ―É –ë–Ψ–Ε–Β―¹―²–≤–Β–Ϋ–Ϋ–Ψ–≥–Ψ –Ω―Ä–Ψ–≤–Η–¥–Β–Ϋ–Η―è, –Ϋ–Ψ –Ψ–Ϋ –Ϋ–Β ―¹–≤―è–Ζ―΄–≤–Α–Μ –Ζ–Α–Κ–Ψ–Ϋ –Ψ–±―Ä–Α―²–Ϋ―΄―Ö –Κ–≤–Α–¥―Ä–Α―²–Ψ–≤ ―¹ –Κ–Ψ–Μ–Η―΅–Β―¹―²–≤–Ψ–Φ –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ¬≠―¹―²–≤–Β–Ϋ–Ϋ―΄―Ö –Η–Ζ–Φ–Β―Ä–Β–Ϋ–Η–Ι. –ü–Η―à–Η –ü–Β–Ι–Μ–Η ―¹―²–Ψ–Μ–Β―²–Η–Β–Φ –Ω–Ψ–Ζ–Ε–Β, –Ω–Ψ¬≠–¥–Ψ–±–Ϋ―΄–Β –Α―Ä–≥―É–Φ–Β–Ϋ―²―΄ –Ψ–Ϋ –±―΄ –Ω―Ä–Η–Φ–Β–Ϋ–Η–Μ –Η –Κ –Α―²–Ψ–Φ–Α–Φ: ―ç–Μ–Β–Κ―²―Ä–Ψ–Ϋ―΄ –Ϋ–Β –Φ–Ψ–≥–Μ–Η –±―΄ ―¹―É―â–Β―¹―²–≤–Ψ–≤–Α―²―¨ –≤ ―É―¹―²–Ψ–Ι―΅–Η–≤―΄―Ö ¬Ϊ―¹–≤―è–Ζ–Α–Ϋ–Ϋ―΄―Ö ―¹–Ψ―¹―²–Ψ―è–Ϋ–Η―è―Ö¬Μ, –Β―¹–Μ–Η –±―΄ ―ç–Μ–Β–Κ―²―Ä–Η―΅–Β―¹–Κ–Η–Β ―¹–Η–Μ―΄ –Ω–Ψ–¥―΅–Η–Ϋ―è–Μ–Η―¹―¨ –Ζ–Α–Κ–Ψ–Ϋ―É –Ψ–±―Ä–Α―²–Ϋ―΄―Ö –Κ―É–±–Ψ–≤. –ù–Α –¥–Α–Ϋ–Ϋ―΄–Ι –Φ–Ψ–Φ–Β–Ϋ―² –Ϋ–Η –Ψ–¥–Η–Ϋ –Η–Ζ ―³–Α–Κ―²–Ψ–≤ –Ψ –£―¹–Β–Μ–Β–Ϋ–Ϋ–Ψ–Ι, –≤ –Κ–Ψ―²–Ψ―Ä–Ψ–Ι –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Ψ –Η–Φ–Β–Β―² –¥–Ψ–Ω–Ψ–Μ–Ϋ–Η―²–Β–Μ―¨–Ϋ―΄–Β –Η–Ζ–Φ–Β―Ä–Β¬≠–Ϋ–Η―è, –Ϋ–Β –Κ–Α–Ε–Β―²―¹―è –Α–±―¹―É―Ä–¥–Ϋ―΄–Φ: ―¹–Ψ–≥–Μ–Α―¹–Ϋ–Ψ ―²–Β–Ψ―Ä–Η–Η ―¹―É–Ω–Β―Ä―¹―²―Ä―É–Ϋ, –≤ ―¹–≤–Β―Ä―Ö―é–Ϋ–Ψ–Ι –£―¹–Β–Μ–Β–Ϋ–Ϋ–Ψ–Ι –Η–Ζ–Φ–Β―Ä–Β–Ϋ–Η–Ι –±―΄–Μ–Ψ –¥–Β―¹―è―²―¨ –Η–Μ–Η –Ψ–¥–Η–Ϋ¬≠–Ϋ–Α–¥―Ü–Α―²―¨. –¦–Η―à–Ϋ–Η–Β –Η–Ζ–Φ–Β―Ä–Β–Ϋ–Η―è, –≤–Ψ–Ζ–Φ–Ψ–Ε–Ϋ–Ψ, –Ω―Ä–Ψ―¹―²–Ψ –Ϋ–Β ―Ä–Α―¹―à–Η¬≠―Ä–Η–Μ–Η―¹―¨ –Ϋ–Α―Ä–Α–≤–Ϋ–Β ―¹ –Ψ―¹―²–Α–Μ―¨–Ϋ―΄–Φ–Η, –Α ―¹–≤–Β―Ä–Ϋ―É–Μ–Η―¹―¨ –Η ¬Ϊ–Κ–Ψ–Φ–Ω–Α–Κ―²–Η―³–Η―Ü–Η―Ä–Ψ–≤–Α–Μ–Η―¹―¨¬Μ. –ï―¹–Μ–Η –Μ–Η―à–Ϋ–Η–Β –Η–Ζ–Φ–Β―Ä–Β–Ϋ–Η―è ―¹–≤–Β―Ä–Ϋ―É–Μ–Η―¹―¨ –≤ –Φ–Α―¹¬≠―à―²–Α–±–Β –ü–Μ–Α–Ϋ–Κ–Α, ―²–Ψ –Ψ–Ϋ–Η –Ϋ–Β –Ψ–Κ–Α–Ζ–Α–Μ–Η –±―΄ –Ω―Ä―è–Φ–Ψ–≥–Ψ –≤–Μ–Η―è–Ϋ–Η―è –Ϋ–Η –Ϋ–Α –Ψ–¥–Η–Ϋ ―ç–Κ―¹–Ω–Β―Ä–Η–Φ–Β–Ϋ―². –ù–Ψ –Β―¹―²―¨ –≤–Β―Ä–Ψ―è―²–Ϋ–Ψ―¹―²―¨ ―²–Ψ–≥–Ψ, ―΅―²–Ψ –Φ–Α―¹¬≠―à―²–Α–± ―¹–≤–Β―Ä―²―΄–≤–Α–Ϋ–Η―è, –Ω―É―¹―²―¨ –Η –Φ–Η–Κ―Ä–Ψ―¹–Κ–Ψ–Ω–Η―΅–Β―¹–Κ–Η–Ι, –≤―¹–Β –Ε–Β –Ϋ–Β ―²–Α–Κ –Φ–Α–Μ, –Κ–Α–Κ –¥–Μ–Η–Ϋ–Α –ü–Μ–Α–Ϋ–Κ–Α. –£ ―ç―²–Ψ–Φ ―¹–Μ―É―΅–Α–Β –¥–Ψ–Ω–Ψ–Μ–Ϋ–Η―²–Β–Μ―¨–Ϋ―΄–Β –Η–Ζ–Φ–Β―Ä–Β–Ϋ–Η―è –Φ–Ψ–≥–Μ–Η –±―΄ –Η–Φ–Β―²―¨ ―¹–Μ–Β–¥―¹―²–≤–Η―è, –Η―¹―¹–Μ–Β–¥–Ψ–≤–Α―²―¨ –Κ–Ψ―²–Ψ―Ä―΄–Β –Ω–Ψ–¥ ―¹–Η–Μ―É ―¹–Ω–Β―Ü–Η–Α–Μ–Η―¹―²–Α–Φ –Ω–Ψ ―³–Η–Ζ–Η–Κ–Β ―΅–Α―¹―²–Η―Ü. –ü―Ä–Β–¥–Ω–Ψ–Μ–Ψ–Ε–Η–Φ, –Κ –Ω―Ä–Η–Φ–Β―Ä―É, ―΅―²–Ψ –≤ –Φ–Α―¹―à―²–Α–±–Β –Φ–Β–Ϋ–Β–Β 10-15 ―¹–Φ –≤ –Η–≥―Ä―É –≤―¹―²―É–Ω–Η–Μ–Η –¥–≤–Α –¥–Ψ–Ω–Ψ–Μ–Ϋ–Η―²–Β–Μ―¨–Ϋ―΄―Ö –Η–Ζ–Φ–Β―Ä–Β–Ϋ–Η―è. –Δ–Ψ–≥–¥–Α –Ω―Ä–Η–Ϋ―Ü–Η–Ω ―¹–Η–Μ–Ψ–≤―΄―Ö –Μ–Η–Ϋ–Η–Ι –Λ–Α―Ä–Α–¥–Β―è –≥–Ψ–≤–Ψ―Ä–Η―², ―΅―²–Ψ ―¹–Η–Μ–Α, –¥–Β–Ι―¹―²–≤―É―é―â–Α―è –≤ –Ω―Ä–Β–¥–Β–Μ–Α―Ö ―ç―²–Ψ–≥–Ψ ―Ä–Α–¥–Η―É―¹–Α, –Ω–Ψ–¥―΅–Η–Ϋ―è–Β―²―¹―è –Ζ–Α–Κ–Ψ–Ϋ―É –Ψ–±―Ä–Α―²–Ϋ―΄―Ö –≤–Β–Μ–Η―΅–Η–Ϋ ―΅–Β―²¬≠–≤–Β―Ä―²–Ψ–Ι ―¹―²–Β–Ω–Β–Ϋ–Η, –Α –Ϋ–Β –Ψ–±―΄―΅–Ϋ–Ψ–Φ―É –Ζ–Α–Κ–Ψ–Ϋ―É –Ψ–±―Ä–Α―²–Ϋ―΄―Ö –Κ–≤–Α–¥―Ä–Α―²–Ψ–≤. –£ ―²―Ä–Β―Ö–Φ–Β―Ä–Ϋ–Ψ–Φ –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Β –≥―Ä–Α–≤–Η―²–Α―Ü–Η―è ―¹―²–Α–Ϋ–Ψ–≤–Η―²―¹―è ―¹―²–Ψ–Μ―¨ ―è―Ä–Ψ―¹―²–Ϋ–Ψ–Ι, ―΅―²–Ψ –Κ–≤–Α–Ϋ―²–Ψ–≤―΄–Β ―ç―³―³–Β–Κ―²―΄ –Η–Φ–Β―é―² –Ζ–Ϋ–Α―΅–Β–Ϋ–Η–Β, –Μ–Η―à―¨ –≤ –Φ–Α―¹―à―²–Α–±–Β –¥–Μ–Η–Ϋ―΄ –ü–Μ–Α–Ϋ–Κ–Α, 10-33 ―¹–Φ. –ù–Ψ –Β―¹–Μ–Η –±―΄ –≥―Ä–Α–≤–Η―²–Α―Ü–Η―è –±―΄–Μ–Α –±–Ψ–Μ–Β–Β ―²–Β―¹–Ϋ–Ψ ―¹–≤―è–Ζ–Α–Ϋ–Α ―¹ ―Ä–Α–¥–Η―É―¹–Ψ–Φ, –Ω–Ψ–¥―΅–Η–Ϋ―è―è―¹―¨ –Ζ–Α–Κ–Ψ–Ϋ―É –Ψ–±―Ä–Α―²–Ϋ―΄―Ö –≤–Β–Μ–Η―΅–Η–Ϋ ―΅–Β―²–≤–Β―Ä―²–Ψ–Ι ―¹―²–Β–Ω–Β–Ϋ–Η, –Α –Ϋ–Β –Ζ–Α–Κ–Ψ–Ϋ―É –Ψ–±―Ä–Α―²¬≠–Ϋ―΄―Ö –Κ–≤–Α–¥―Ä–Α―²–Ψ–≤, ―²–Ψ –Κ–≤–Α–Ϋ―²–Ψ–≤―΄–Β ―ç―³―³–Β–Κ―²―΄ –≤–Ψ–Ζ–Ϋ–Η–Κ–Α–Μ–Η –±―΄ –¥–Ψ –¥–Ψ¬≠―¹―²–Η–Ε–Β–Ϋ–Η―è ―Ä–Α–¥–Η―É―¹–Α –≤ 10-33 ―¹–Φ. –ü–Ψ–Μ–Β–Ζ–Ϋ–Α―è –¥–Μ–Η–Ϋ–Α –ü–Μ–Α–Ϋ–Κ–Α –Ϋ–Β –Ψ―¹―²–Α–≤–Α–Μ–Α―¹―¨ –±―΄ –¥–Ψ–Μ–Β–Β ―²–Α–Κ–Ψ–Ι –Κ―Ä–Ψ―à–Β―΅–Ϋ–Ψ–Ι, –Η –¥–Μ―è ―¹–Ψ–Ζ–¥–Α–Ϋ–Η―è –Φ–Α¬≠–Μ–Ψ–Ι ―΅–Β―Ä–Ϋ–Ψ–Ι –¥―΄―Ä―΄ –Ω–Ψ―²―Ä–Β–±–Ψ–≤–Α–Μ–Ψ―¹―¨ –±―΄ –Ϋ–Β ―²–Α–Κ–Α―è –Κ―Ä–Η―²–Η―΅–Β―¹–Κ–Α―è –≤–Β–Μ–Η―΅–Η–Ϋ–Α ―¹–Ε–Α―²–Η―è, –Κ–Α–Κ –≤ –Ψ–±―΄―΅–Ϋ–Ψ–Φ ―²―Ä–Β―Ö–Φ–Β―Ä–Ϋ–Ψ–Φ –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Β. –ù–Β–Κ–Ψ―²–Ψ―Ä―΄–Β ―³–Η–Ζ–Η–Κ–Η ―¹―΅–Η―²–Α―é―², ―΅―²–Ψ –Φ–Α–Μ―΄–Β ―΅–Β―Ä–Ϋ―΄–Β –¥―΄―Ä―΄ –Φ–Ψ–Ε¬≠–Ϋ–Ψ –±―΄–Μ–Ψ –±―΄ ―¹–Ψ–Ζ–¥–Α–≤–Α―²―¨ –¥–Α–Ε–Β –Ϋ–Α ―²–Β―Ö–Ϋ–Η―΅–Β―¹–Κ–Η ―Ä–Β–Α–Μ–Η–Ζ―É–Β–Φ―΄―Ö ―É―¹–Κ–Ψ―Ä–Η―²–Β–Μ―è―Ö. –û–±―â–Β–Η–Ζ–≤–Β―¹―²–Ϋ–Ψ, ―΅―²–Ψ –Ω–Ψ―¹–Μ–Β–¥–Ϋ–Η–Β ―²―Ä–Η–¥―Ü–Α―²―¨ –Μ–Β―² –Ε–Η–Ζ–Ϋ–Η –≠–Ι–Ϋ―à―²–Β–Ι–Ϋ –Ω–Ψ―²―Ä–Α―²–Η–Μ –Ϋ–Α –Ω–Ψ–Η―¹–Κ –Ψ–±―ä–Β–¥–Η–Ϋ–Β–Ϋ–Ϋ–Ψ–Ι ―²–Β–Ψ―Ä–Η–Η ―³–Η–Ζ–Η¬≠―΅–Β―¹–Κ–Η―Ö –Ζ–Α–Κ–Ψ–Ϋ–Ψ–≤. –û–Ϋ –Ζ–Α–Ϋ–Η–Φ–Α–Μ―¹―è ―ç―²–Η–Φ –≤ –Ψ–¥–Η–Ϋ–Ψ―΅–Κ―É; –Ϋ–Ψ –¥―Ä―É–≥–Η–Β ―É―΅–Β–Ϋ―΄–Β, –Η–Ζ –Κ–Ψ―²–Ψ―Ä―΄―Ö ―¹―²–Ψ–Η―² –Ψ―²–Φ–Β―²–Η―²―¨ –Α–Ϋ–≥–Μ–Η–Ι―¹–Κ–Ψ–≥–Ψ –Α―¹―²―Ä–Ψ―³–Η¬≠–Ζ–Η–Κ–Α –ê―Ä―²―É―Ä–Α –≠–¥–¥–Η–Ϋ–≥―²–Ψ–Ϋ–Α, ―²–Α–Κ–Ε–Β –Ω–Ψ –Ψ―²–¥–Β–Μ―¨–Ϋ–Ψ―¹―²–Η ―¹―Ä–Α–Ε–Α–Μ–Η―¹―¨ ―¹ ―ç―²–Ψ–Ι –Ω―Ä–Ψ–±–Μ–Β–Φ–Ψ–Ι. (–≠–¥–¥–Η–Ϋ–≥―²–Ψ–Ϋ, ―É–Ε–Β –Ω―Ä–Ψ―¹–Μ–Α–≤–Η–≤―à–Η―¹―¨ –Κ–Μ–Α―¹―¹–Η―΅–Β―¹–Κ–Η–Φ –Η –Ϋ–Α–¥–Β–Ε–Ϋ―΄–Φ ―²―Ä―É–¥–Ψ–Φ –Ω–Ψ ―²–Β–Ψ―Ä–Η–Η –Ψ―²–Ϋ–Ψ―¹–Η―²–Β–Μ―¨–Ϋ–Ψ―¹―²–Η –Η –Ζ–≤–Β–Ζ–¥–Ϋ–Ψ–Ι ―¹―²―Ä―É–Κ―²―É―Ä–Β, –≤ –Ω–Ψ–Ζ–¥–Ϋ–Η–Β –≥–Ψ–¥―΄ –Ε–Η–Ζ–Ϋ–Η ―¹―²―Ä–Α―¹―²–Ϋ–Ψ ―É–≤–Μ–Β–Κ¬≠―¹―è –Ϋ―É–Φ–Β―Ä–Ψ–Μ–Ψ–≥–Η―΅–Β―¹–Κ–Ψ–Ι ¬Ϊ―³―É–Ϋ–¥–Α–Φ–Β–Ϋ―²–Α–Μ―¨–Ϋ–Ψ–Ι ―²–Β–Ψ―Ä–Η–Β–Ι¬Μ, –≤ ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Η–Η ―¹ –Κ–Ψ―²–Ψ―Ä–Ψ–Ι –Ϋ–Α―à–Α –£―¹–Β–Μ–Β–Ϋ–Ϋ–Α―è –Ζ–Α–Φ–Κ–Ϋ―É―²–Α –Η –Κ–Ψ–Ϋ–Β―΅–Ϋ–Α. –û–Ϋ –¥–Α–Ε–Β –Ω―Ä–Β–¥–Μ–Ψ–Ε–Η–Μ ―³–Ψ―Ä–Φ―É–Μ―É ―Ä–Α―¹―΅–Β―²–Α ―²–Ψ―΅–Ϋ–Ψ–≥–Ψ –Κ–Ψ–Μ–Η―΅–Β―¹―²–≤–Α –Α―²–Ψ–Φ–Ψ–≤ –≤–Ψ –£―¹–Β–Μ–Β–Ϋ–Ϋ–Ψ–Ι.)*** –≠―²–Η –Ω–Ψ–Ω―΄―²–Κ–Η –±―΄–Μ–Η –Ω―Ä–Β–Ε–¥–Β–≤―Ä–Β–Φ–Β–Ϋ–Ϋ―΄ –Ω–Ψ –Φ–Ϋ–Ψ–≥–Η–Φ –Ω―Ä–Η¬≠―΅–Η–Ϋ–Α–Φ. –ù–Α–Ω―Ä–Η–Φ–Β―Ä, –Η―¹―¹–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ–Η ―É―΅–Η―²―΄–≤–Α–Μ–Η –≥―Ä–Α–≤–Η―²–Α―Ü–Η―é –Η ―ç–Μ–Β–Κ―²―Ä–Ψ–Φ–Α–≥–Ϋ–Η―²–Ϋ―΄–Β ―¹–Η–Μ―΄, –Ϋ–Β –Ω―Ä–Η–Ϋ–Η–Φ–Α―è –≤ ―Ä–Α―¹―΅–Β―² –¥―Ä―É–≥–Η–Β ―¹–Η¬≠–Μ―΄: ―¹–Η–Μ―¨–Ϋ–Ψ–Β ―è–¥–Β―Ä–Ϋ–Ψ–Β –≤–Ζ–Α–Η–Φ–Ψ–¥–Β–Ι―¹―²–≤–Η–Β –Η ―²–Α–Κ –Ϋ–Α–Ζ―΄–≤–Α–Β–Φ–Ψ–Β ―¹–Μ–Α¬≠–±–Ψ–Β –≤–Ζ–Α–Η–Φ–Ψ–¥–Β–Ι―¹―²–≤–Η–Β, –≤–Α–Ε–Ϋ–Ψ–Β –¥–Μ―è –Ϋ–Β–Ι―²―Ä–Η–Ϋ–Ψ –Η ―Ä–Α–¥–Η–Ψ–Α–Κ―²–Η–≤¬≠–Ϋ–Ψ―¹―²–Η. –ë―΄–Μ–Η –Η –¥―Ä―É–≥–Η–Β –Μ–Ψ–Ε–Ϋ―΄–Β –Ψ–Ζ–Α―Ä–Β–Ϋ–Η―è. –ù–Ψ ―²–Β–Ω–Β―Ä―¨ ―É –Ϋ–Α―¹ –Β―¹―²―¨ ―¹–Η–Μ―¨–Ϋ–Α―è ―É–≤–Β―Ä–Β–Ϋ–Ϋ–Ψ―¹―²―¨ –≤ ―²–Ψ–Φ, ―΅―²–Ψ ―²–Β–Ψ―Ä–Η―è ―¹―É–Ω–Β―Ä―¹―²―Ä―É–Ϋ, –Η–Μ–Η ―²–Ψ, ―΅―²–Ψ ―¹–Β–Ι―΅–Α―¹ –Ϋ–Α–Ζ―΄–≤–Α―é―² –€-―²–Β–Ψ―Ä–Η–Β–Ι, –Ψ―²–Κ―Ä―΄–≤–Α–Β―² –Ω―É―²―¨ –Κ ―³―É–Ϋ–¥–Α–Φ–Β–Ϋ―²–Α–Μ―¨–Ϋ―΄–Φ ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η―è–Φ. (–ù–Β–Κ–Ψ―²–Ψ―Ä―΄–Β ―¹–Ω–Β―Ü–Η–Α–Μ–Η―¹―²―΄ ―É–Ω–Ψ–¥–Ψ–±–Μ―è―é―² ―¹–Β–≥–Ψ–¥–Ϋ―è―à–Ϋ―é―é ―¹–Η―²―É–Α―Ü–Η―é ―¹–Ψ―¹―²–Ψ―è–Ϋ–Η―é –Κ–≤–Α–Ϋ―²–Ψ–≤–Ψ–Ι ―²–Β–Ψ―Ä–Η–Η –¥–Ψ 1925 –≥–Ψ–¥–Α, –Κ–Ψ–≥–¥–Α –≤―¹–Β –Ω–Ψ–Ϋ–Η–Φ–Α–Μ–Η –Ϋ–Β–Ψ–±―Ö–Ψ–¥–Η–Φ–Ψ―¹―²―¨ –Ϋ–Ψ¬≠–≤–Ψ–Ι –Ω–Α―Ä–Α–¥–Η–≥–Φ―΄, –Ϋ–Ψ –≤ ―É–Φ–Α―Ö –≤–Ψ–Ζ–Ϋ–Η–Κ–Α–Μ–Η ―²–Ψ–Μ―¨–Κ–Ψ –Β–Β –Ω―Ä–Ψ–±–Μ–Β―¹–Κ–Η.) –Δ–Β–Ψ―Ä–Η–Η –£–Β–Μ–Η–Κ–Ψ–≥–Ψ –Ψ–±―ä–Β–¥–Η–Ϋ–Β–Ϋ–Η―è ―²–Β–Ω–Β―Ä―¨ –Ω―Ä–Η–≤–Μ–Β–Κ–Α―é―² –Φ–Ψ–Μ–Ψ–¥―΄―Ö ―É―΅–Β–Ϋ―΄―Ö, –Α –Ϋ–Β ―²–Ψ–Μ―¨–Κ–Ψ –Ω―Ä–Η–Ζ–Ϋ–Α–Ϋ–Ϋ―΄―Ö ―¹–≤–Β―²–Η–Μ, –Κ–Ψ―²–Ψ―Ä―΄–Β –Φ–Ψ–≥―É―² –Ω–Ψ–Ζ¬≠–≤–Ψ–Μ–Η―²―¨ ―¹–Β–±–Β ―Ä–Η―¹–Κ–Ϋ―É―²―¨, –Ω–Β―Ä–Β–Ω―Ä―΄–≥–Ϋ―É–≤ ―΅–Β―Ä–Β–Ζ ―¹–Β–±―è –Η –Ϋ–Η―΅–Β–≥–Ψ –Ϋ–Β –¥–Ψ―¹―²–Η–≥–Ϋ―É–≤. –Γ―É―â–Β―¹―²–≤―É–Β―² –Ψ–≥―Ä–Ψ–Φ–Ϋ–Α―è –Ω―Ä–Ψ–Ω–Α―¹―²―¨ –Φ–Β–Ε–¥―É –Μ–Α–±–Η―Ä–Η–Ϋ―²–Ψ–Φ –¥–Β¬≠―¹―è―²–Η –Η–Μ–Η –Ψ–¥–Η–Ϋ–Ϋ–Α–¥―Ü–Α―²–Η –Η–Ζ–Φ–Β―Ä–Β–Ϋ–Η–Ι –Η ―²–Β–Φ, ―΅―²–Ψ –Φ–Ψ–Ε–Ϋ–Ψ –Ϋ–Α–±–Μ―é¬≠–¥–Α―²―¨ –Η–Μ–Η –Η–Ζ–Φ–Β―Ä–Η―²―¨. –ù–Β ―è―¹–Ϋ–Ψ, ―΅―²–Ψ –Ε–Β –Ψ–Ω―Ä–Β–¥–Β–Μ―è–Β―² –≥–Β–Ψ–Φ–Β―²―Ä–Η―é ¬Ϊ–Ψ–±―΄―΅–Ϋ–Ψ–≥–Ψ¬Μ –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Α: –Ω–Ψ―΅–Β–Φ―É –≤ –Ϋ–Α―à–Β–Ι –£―¹–Β–Μ–Β–Ϋ–Ϋ–Ψ–Ι ―Ä–Α–Ζ¬≠–≤–Β―Ä–Ϋ―É–Μ–Η―¹―¨ ―²–Ψ–Μ―¨–Κ–Ψ ―²―Ä–Η –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Β–Ϋ–Ϋ―΄―Ö –Η–Ζ–Φ–Β―Ä–Β–Ϋ–Η―è? –Δ–Β–Ψ―Ä–Β¬≠―²–Η–Κ–Η –¥–Ψ ―¹–Η―Ö –Ω–Ψ―Ä –Ϋ–Β –Φ–Ψ–≥―É―² –Ψ―²–≤–Β―²–Η―²―¨, –≤―¹–Β –Μ–Η –¥–Ψ–Ω–Ψ–Μ–Ϋ–Η―²–Β–Μ―¨–Ϋ―΄–Β –Η–Ζ–Φ–Β―Ä–Β–Ϋ–Η―è ―¹–≤–Β―Ä–Ϋ―É―²―΄ –≤ –Φ–Η–Κ―Ä–Ψ―¹–Κ–Ψ–Ω–Η―΅–Β―¹–Κ–Η―Ö –Φ–Α―¹―à―²–Α–±–Α―Ö, –Η–Μ–Η –Ε–Β –≤–Ψ–Ζ–Φ–Ψ–Ε–Ϋ–Ψ ―¹―É―â–Β―¹―²–≤–Ψ–≤–Α–Ϋ–Η–Β –¥―Ä―É–≥–Η―Ö –≤―¹–Β–Μ–Β–Ϋ–Ϋ―΄―Ö, –Ψ―²–¥–Β–Μ–Β–Ϋ¬≠–Ϋ―΄―Ö –Ψ―² –Ϋ–Α―à–Β–Ι –≤ –Ϋ–Β–Κ–Ψ–Φ–Ω–Α–Κ―²–Η―³–Η―Ü–Η―Ä–Ψ–≤–Α–Ϋ–Ϋ–Ψ–Φ –¥–Ψ–Ω–Ψ–Μ–Ϋ–Η―²–Β–Μ―¨¬≠–Ϋ–Ψ–Φ –Η–Ζ–Φ–Β―Ä–Β–Ϋ–Η–Η, –Ω–Ψ–¥–Ψ–±–Ϋ–Ψ ―²–Ψ–Φ―É, –Κ–Α–Κ –≤ –Ϋ–Α―à–Β–Φ ―²―Ä–Β―Ö–Φ–Β―Ä–Ϋ–Ψ–Φ –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Β –Φ–Ψ–Ε–Β―² ―¹―É―â–Β―¹―²–≤–Ψ–≤–Α―²―¨ –Φ–Ϋ–Ψ–Ε–Β―¹―²–≤–Ψ –¥–≤―É―Ö–Φ–Β―Ä–Ϋ―΄―Ö –Ω–Μ–Ψ―¹–Κ–Ψ―¹―²–Β–Ι, –Ϋ–Β ―¹–Ψ–Ω―Ä–Η–Κ–Α―¹–Α―é―â–Η―Ö―¹―è –¥―Ä―É–≥ ―¹ –¥―Ä―É–≥–Ψ–Φ. (–£–Ψ–Ω―Ä–Ψ―¹ –Ψ ―²–Ψ–Φ, –Φ–Ψ–Ε–Β―² –Μ–Η –≤–Ψ –£―¹–Β–Μ–Β–Ϋ–Ϋ–Ψ–Ι –±―΄―²―¨ –±–Ψ–Μ–Β–Β –Ψ–¥–Ϋ–Ψ–≥–Ψ –≤―Ä–Β–Φ–Β–Ϋ–Ϋó–≥–Ψ –Η–Ζ–Φ–Β―Ä–Β–Ϋ–Η―è, –Φ–Β–Ϋ–Β–Β –Ω―Ä―è–Φ–Ψ–Μ–Η–Ϋ–Β–Β–Ϋ. –î–Μ―è –Ψ–Ω–Η―¹–Α–Ϋ–Η―è –Ω―Ä–Ψ¬≠–Η―¹―Ö–Ψ–¥―è―â–Β–≥–Ψ –≤ –Ϋ–Β–Φ –Ϋ―É–Ε–Β–Ϋ –±–Ψ–Μ–Β–Β –±–Ψ–≥–Α―²―΄–Ι ―è–Ζ―΄–Κ, ―¹–Ψ–¥–Β―Ä–Ε–Α―â–Η–Ι –±–Ψ–Μ―¨―à–Β–Β –Κ–Ψ–Μ–Η―΅–Β―¹―²–≤–Ψ –≤―Ä–Β–Φ–Β–Ϋ–Ϋ―¨í―Ö ―³–Ψ―Ä–Φ.) –£ –Ψ–±―â–Β–Φ, –Ϋ–Β–Ψ–±―Ö–Ψ–¥–Η–Φ―É―é ―³–Η–Ζ–Η–Κ–Α–Φ –Φ–Α―²–Β–Φ–Α―²–Η–Κ―É –Φ–Ψ–Ε–Ϋ–Ψ ¬Ϊ―¹–Ϋ―è―²―¨ ―¹ –Ω–Ψ–Μ–Κ–Η¬Μ. –ù–Β–Β–≤–Κ–Μ–Η–¥–Ψ–≤–Α –≥–Β–Ψ–Φ–Β―²―Ä–Η―è, –Η―¹–Ω–Ψ–Μ―¨–Ζ–Ψ–≤–Α–Ϋ¬≠–Ϋ–Α―è –≠–Ι–Ϋ―à―²–Β–Ι–Ϋ–Ψ–Φ –¥–Μ―è –Ψ–Ω–Η―¹–Α–Ϋ–Η―è –Η―¹–Κ―Ä–Η–≤–Μ–Β–Ϋ–Ϋ―΄―Ö –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤, ―Ä–Α–Ζ―Ä–Α–±–Ψ―²–Α–Ϋ–Α –†–Η–Φ–Α–Ϋ–Ψ–Φ –Η –Ω―Ä–Ψ―΅–Η–Φ–Η; –Ω–Η–Ψ–Ϋ–Β―Ä―΄ –Κ–≤–Α–Ϋ―²–Ψ–≤–Ψ–Ι ―²–Β–Ψ¬≠―Ä–Η–Η ―²–Α–Κ–Ε–Β –Ψ–±–Ϋ–Α―Ä―É–Ε–Η–Μ–Η –Φ–Α―²–Β–Φ–Α―²–Η―΅–Β―¹–Κ–Η–Β –≤―΄–Κ–Μ–Α–¥–Κ–Η –¥–Β–≤―è―²–Ϋ–Α¬≠–¥―Ü–Α―²–Ψ–≥–Ψ –≤–Β–Κ–Α, ―É–¥–Ψ–≤–Μ–Β―²–≤–Ψ―Ä―è―é―â–Η–Β –Η―Ö ―Ü–Β–Μ―è–Φ. –ù–Ψ ―²–Β–Ψ―Ä–Β―²–Η–Κ–Α–Φ, ―Ä–Α–±–Ψ―²–Α―é―â–Η–Φ ―¹–Ψ ―¹―²―Ä―É–Ϋ–Α–Φ–Η, –Ϋ―É–Ε–Ϋ–Α –Φ–Α―²–Β–Φ–Α―²–Η–Κ–Α –¥–≤–Α–¥―Ü–Α―²―¨ –Ω–Β―Ä¬≠–≤–Ψ–≥–Ψ ―¹―²–Ψ–Μ–Β―²–Η―è. –Δ–Β–Ψ―Ä–Η―è ―¹―É–Ω–Β―Ä―¹―²―Ä―É–Ϋ –Ω–Ψ–Κ–Α –Ϋ–Β –≤ ―¹–Ψ―¹―²–Ψ―è–Ϋ–Η–Η –Ψ–±―ä―è―¹–Ϋ–Η―²―¨ ―Ä–Α–Ζ¬≠–Μ–Η―΅–Ϋ―΄–Β ―²–Η–Ω―΄ ―¹―É–±–Α―²–Ψ–Φ–Ϋ―΄―Ö ―΅–Α―¹―²–Η―Ü βÄî –Κ–≤–Α―Ä–Κ–Η, –≥–Μ―é–Ψ–Ϋ―΄ –Η ―².–Ω. βÄî –Η –≤―¹–Β –Β―â–Β –Ϋ–Β –Ω―Ä–Β–¥―¹–Κ–Α–Ζ–Α–Μ–Α –Ϋ–Η―΅–Β–≥–Ψ –Ϋ–Ψ–≤–Ψ–≥–Ψ, –Ϋ–Η –≤ ―ç–Κ―¹–Ω–Β―Ä–Η–Φ–Β–Ϋ―²–Α–Μ―¨–Ϋ–Ψ–Φ, –Ϋ–Η –≤ –Κ–Ψ―¹–Φ–Ψ–Μ–Ψ–≥–Η―΅–Β―¹–Κ–Ψ–Φ ―¹–Φ―΄―¹–Μ–Β, ―΅―²–Ψ ―¹–Μ–Β–¥–Ψ–≤–Α–Μ–Ψ –±―΄ –Η–Ζ –¥–Ψ–Ω–Ψ–Μ–Ϋ–Η―²–Β–Μ―¨–Ϋ―΄―Ö –Η–Ζ–Φ–Β―Ä–Β–Ϋ–Η–Ι. –ù–Ψ –Φ–Ϋ–Ψ–≥–Η–Β –≥–Ψ―²–Ψ–≤―΄ ―¹―²–Α¬≠–≤–Η―²―¨ –Ϋ–Α –Ϋ–Β–Β, –Ψ―²―΅–Α―¹―²–Η –Ω–Ψ―²–Ψ–Φ―É, ―΅―²–Ψ –Ψ–Ϋ–Α –Ω–Ψ―΅―²–Η ¬Ϊ–Ω―Ä–Β–¥―¹–Κ–Α–Ζ―΄–≤–Α–Β―²¬Μ –Ϋ–Β–Ψ–±―Ö–Ψ–¥–Η–Φ–Ψ―¹―²―¨ ―¹―É―â–Β―¹―²–≤–Ψ–≤–Α–Ϋ–Η―è ―¹–Η–Μ―΄, –Ω–Ψ–¥–Ψ–±–Ϋ–Ψ–Ι –≥―Ä–Α–≤–Η―²–Α―Ü–Η–Η, –Η –Ψ―²―΅–Α―¹―²–Η –Η–Ζ ―ç―¹―²–Β―²–Η―΅–Β―¹–Κ–Η―Ö ―¹–Ψ–Ψ–±―Ä–Α–Ε–Β–Ϋ–Η–Ι. –ü–Ψ–¥–Ψ–±–Ϋ–Α―è –Ω–Ψ–Ζ–Η¬≠―Ü–Η―è –Η–Φ–Β–Β―² ―¹–≤–Ψ–Η –Ω―Ä–Β―Ü–Β–¥–Β–Ϋ―²―΄. –≠–Ι–Ϋ―à―²–Β–Ι–Ϋ–Ψ–≤–Α ―²–Β–Ψ―Ä–Η―è –≥―Ä–Α–≤–Η¬≠―²–Α―Ü–Η–Η βÄî –Ψ–±―â–Α―è ―²–Β–Ψ―Ä–Η―è –Ψ―²–Ϋ–Ψ―¹–Η―²–Β–Μ―¨–Ϋ–Ψ―¹―²–Η βÄî –Ϋ–Α―à–Μ–Α ―à–Η―Ä–Ψ–Κ–Ψ–Β –Ω―Ä–Η–Ζ–Ϋ–Α–Ϋ–Η–Β –Η–Φ–Β–Ϋ–Ϋ–Ψ –≤ ―¹–Η–Μ―É ―¹–≤–Ψ–Β–Ι ―ç―¹―²–Β―²–Η―΅–Β―¹–Κ–Ψ–Ι –Ω―Ä–Η―²―è–≥–Α―²–Β–Μ―¨¬≠–Ϋ–Ψ―¹―²–Η, ―Ö–Ψ―²―è –Β–Β ―ç–Φ–Ω–Η―Ä–Η―΅–Β―¹–Κ–Η–Β –Ω–Ψ–¥―²–≤–Β―Ä–Ε–¥–Β–Ϋ–Η―è –±―΄–Μ–Η –Ζ―΄–±–Κ–Η–Φ–Η –Η –Ϋ–Β―²–Ψ―΅–Ϋ―΄–Φ–Η. –û–Ϋ–Α –Ω―Ä–Β–≤–Ζ–Ψ―à–Μ–Α ―²–Β–Ψ―Ä–Η―é –ù―¨―é―²–Ψ–Ϋ–Α, –Ω―Ä–Β–¥–Μ–Ψ–Ε–Η–≤ –±–Ψ–Μ–Β–Β –≥–Μ―É–±–Ψ–Κ–Ψ–Β –Ω–Ψ–Ϋ–Η–Φ–Α–Ϋ–Η–Β. –≠–Ι–Ϋ―à―²–Β–Ι–Ϋ, –≤ –Ψ―²–Μ–Η―΅–Η–Β –Ψ―² –ù―¨―é¬≠―²–Ψ–Ϋ–Α, –Β―¹―²–Β―¹―²–≤–Β–Ϋ–Ϋ―΄–Φ –Ψ–±―Ä–Α–Ζ–Ψ–Φ –Ψ–±―ä―è―¹–Ϋ―è–Μ, –Ω–Ψ―΅–Β–Φ―É –≤―¹–Β –Ω–Α–¥–Α–Β―² ―¹ –Ψ–¥–Η–Ϋ–Α–Κ–Ψ–≤–Ψ–Ι ―¹–Κ–Ψ―Ä–Ψ―¹―²―¨―é –Η –Ω–Ψ―΅–Β–Φ―É –≥―Ä–Α–≤–Η―²–Α―Ü–Η―è –Ω–Ψ–¥―΅–Η–Ϋ―è–Β―²―¹―è –Ζ–Α–Κ–Ψ–Ϋ―É –Ψ–±―Ä–Α―²–Ϋ―΄―Ö –Κ–≤–Α–¥―Ä–Α―²–Ψ–≤. –û–±―â–Α―è ―²–Β–Ψ―Ä–Η―è –Ψ―²–Ϋ–Ψ―¹–Η―²–Β–Μ―¨–Ϋ–Ψ¬≠―¹―²–Η –¥–Α―²–Η―Ä―É–Β―²―¹―è 1916 –≥–Ψ–¥–Ψ–Φ; –Ψ–Ϋ–Α –Ψ–±―ä―è―¹–Ϋ–Η–Μ–Α –¥–Ψ―¹–Β–Μ–Β –Ϋ–Β―è―¹–Ϋ―É―é –Α–Ϋ–Ψ–Φ–Α–Μ–Η―é –≤ –Ψ―Ä–±–Η―²–Β –€–Β―Ä–Κ―É―Ä–Η―è. –≠―²–Ψ –Ψ–±―ä―è―¹–Ϋ–Β–Ϋ–Η–Β –Ω–Ψ–Μ―É―΅–Η–Μ–Ψ –Ζ–Ϋ–Α–Φ–Β–Ϋ–Η―²–Ψ–Β –Ω–Ψ–¥―²–≤–Β―Ä–Ε–¥–Β–Ϋ–Η–Β –Ω―Ä–Η –Η–Ζ–Φ–Β―Ä–Β–Ϋ–Η–Η –Ψ―²–Κ–Μ–Ψ–Ϋ–Β–Ϋ–Η―è ―¹–≤–Β¬≠―²–Α –Ζ–≤–Β–Ζ–¥―΄ –≤–Ψ –≤―Ä–Β–Φ―è –Ζ–Α―²–Φ–Β–Ϋ–Η―è –≤ 1919 –≥–Ψ–¥―É, –Ϋ–Ψ ―¹–Α–Φ –≠–Ι–Ϋ―à―²–Β–Ι–Ϋ –±―΄–Μ ―É–≤–Β―Ä–Β–Ϋ –≤ ―¹–≤–Ψ–Β–Φ –¥–Β―²–Η―â–Β –≤―¹–Μ–Β–¥―¹―²–≤–Η–Β –Β–≥–Ψ –Η–Ζ―è―â–Ϋ–Ψ―¹―²–Η: –Κ–Ψ¬≠–≥–¥–Α –Β–≥–Ψ ―¹–Ω―Ä–Ψ―¹–Η–Μ–Η, –Κ–Α–Κ –±―΄ –Ψ–Ϋ –Ψ―²―Ä–Β–Α–≥–Η―Ä–Ψ–≤–Α–Μ, –Β―¹–Μ–Η –±―΄ –Ζ–Α―²–Φ–Β–Ϋ–Η–Β –Ϋ–Β –Ω–Ψ–¥―²–≤–Β―Ä–¥–Η–Μ–Ψ –Β–≥–Ψ ―²–Β–Ψ―Ä–Η―é, –Ψ–Ϋ –Ψ―²–≤–Β―²–Η–Μ, ―΅―²–Ψ –Β–Φ―É –±―΄–Μ–Ψ –±―΄ ¬Ϊ–Ε–Α–Μ―¨ –™–Ψ―¹–Ω–Ψ–¥–Α –ë–Ψ–≥–Α¬Μ. |
| –ß–Η―²–Α–Ι―²–Β: |
|---|